اختبار النسبة (رياضيات)

في الرياضيات، اختبار النسبة (بالإنجليزية: Ratio test)‏ هو اختبار يحدد تقارب المتسلسلة $\sum _{n=1}^{\mathrm{\infty }}{a}_n$ من عدمه، حيث $a_n$ هو عدد حقيقي أو عقدي لا يساوي الصفر عندما يصير n كبيرا. أول من نشر هذا الاختبار هو عالم الرياضيات الفرنسي لورن دالمبير.

الاختبار

شجرة القرار المتعلقة باختبار النسبة

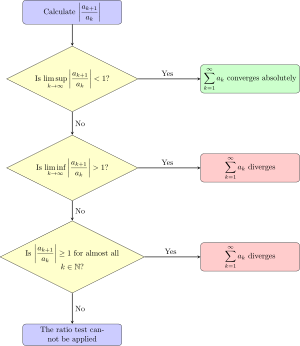
يستعمل الشكل الاعتيادي لهذه الاختبار النهاية التالية:

$L=\underset{n\to \mathrm{\infty }}{\lim }\left|\frac{a_{n+1}}{a_n}\right|.$

(1)

ينص الاختبار على ما يلي:

• إذا كان L < 1 فإن المتسلسلة تتقارب مطلقا.
• إذا كان L > 1 فإن المتسلسلة تتباعد.
• إذا كان L = 1 أو لم تكن هذه النهاية موجودة، فإنه لا جدوى من هذا الاختبار لأن هناك متسلسلات متقاربات يحققن هذا الشرط ولكن هناك أيضا متسلسلات متباعدات أيضا يحققنه.

أمثلة

متقاربة لأن L < 1

لتكن المتسلسلة التالية :

$\sum _{n=1}^{\mathrm{\infty }}\frac{n}{e^n}$

استعمال اختبار النسبة يعطي النهاية التالية :

$L=\underset{n\to \mathrm{\infty }}{\lim }\left|\frac{a_{n+1}}{a_n}\right|=\underset{n\to \mathrm{\infty }}{\lim }\left|\frac{\frac{n+1}{e^{n+1}}}{\frac{n}{e^n}}\right|=\frac{1}{e}<1.$

بما أن هذه النهاية هي أصغر قطعا من الواحد، فإن المتسلسلة تتقارب.

متباعدة لأن L > 1

لتكن المتسلسلة التالية :

$\sum _{n=1}^{\mathrm{\infty }}\frac{e^n}{n}.$

استعمال اختبار النسبة يعطي النهاية التالية :

$L=\underset{n\to \mathrm{\infty }}{\lim }\left|\frac{a_{n+1}}{a_n}\right|=\underset{n\to \mathrm{\infty }}{\lim }\left|\frac{\frac{e^{n+1}}{n+1}}{\frac{e^n}{n}}\right|=e>1.$

بما أن هذه النهاية هي أكبر قطعا من الواحد، فإن المتسلسلة تتباعد.

بدون جدوى لأن L = 1

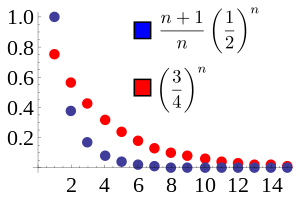
لتكن المتسلسلات الثلاث التالية:

$\sum _{n=1}^{\mathrm{\infty }}1,$

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2},$

$\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}.$

البرهان

In this example, the ratio of adjacent terms in the blue sequence converges to L=1/2. We choose r = (L+1)/2 = 3/4. Then the blue sequence is dominated by the red sequence r^k for all n ≥ 2. The red sequence converges, so the blue sequence does as well.

$\sum _{i=N+1}^{\mathrm{\infty }}\left|a_i\right|=\sum _{i=1}^{\mathrm{\infty }}\left|a_{N+i}\right|<\sum _{i=1}^{\mathrm{\infty }}{r}^i\left|a_N\right|=\left|a_N\right|\sum _{i=1}^{\mathrm{\infty }}{r}^i=\left|a_N\right|\frac{r}{1-r}<\mathrm{\infty }.$

انظر أيضا

• نصف قطر التقارب