|
تضامنًا مع حق الشعب الفلسطيني |
مرافق زاوي


في الهندسة الرياضية، المرافق الزاوي أو الوتر المقترن هو تحويل هندسي لكائن يكون عادةً بانعكاسه حول منصفات زوايا. يُعرّف المرافق الزاوي لنقطةٍ ما بالنسبة لمثلث على أنها نقطة تقاطع انعكاسات المستقيمات الواصلة بين النقطة الأصلية ورؤوس المثلث مع منصفات رؤوس هذه المثلث على الترتيب. رياضياً، المرافق الزاوي لنقطةٍ ما بالنسبة للمثلث هو تقاطع انعكاسات الخطوط المستقيمة حول منصفات الزوايا على الترتيب. يُشار إلى المرافق الزاوي للنقطة بالترميز: والمرافق الزاوي للنقطة هو نقطة الأصل . بينما بالنسبة للخط المستقيم المار بأحد رؤوس المثلث، فيُعرّف المرافق الزاوي له على أنه انعكاس هذا الخط حول منصف زاوية رأس المثلث المار به.[1]
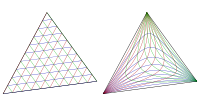
حالات خاصة
المرافق الزاوي لمركز الدائرة الداخلية هو نفسه. بشكلٍ مكافئِ، المرافق الزاوي لمنصف زاوية مثلث هو نفسه أيضاً. المرافق الزاوي لنقطة تقاطع ارتفاعات المثلث هو مركز دائرة المثلث المحيطة .[1]
في القطوع المخروطية
لاهليلج ∆ (دلتا)، إذا كل منهما يمر بقطب الآخر. مثلاً في الشكل المرفق: الخط القطبي p للنقطة القطبية P يمر بالقطب R للخط r الذي بدوره يمر بالقطب P. كذلك كل نقطة P يمكن أن تسمى قطب لدلتا والخط p المار بنقاط المماس T1 T2 يسمى خط قطبي للنقطة P بالنسبة لدلتا. بالإشارة إلى دالة التقابل (Bijection)، الخط القطبي هو الخط المشترك في دالة الالتفاف (Involution) بين الإسقاطات المتطابقة لمقطعين مستويين لنفس المخروط (Quadric). في هذة الحالة القطب ب هو مركز الالتفاف. بالإشارة إلى نفس الشكل المرفق، نقطه تقاطع M القطبتين r p هي قطب الخط المار بالقطبين [2] P R
انظر أيضاً
مراجع
- ^ أ ب صابر، طارق؛ أندريكا، دورين (1434هـ). رياضيَّات الأولمبياد، الهندسة، الجزء الأول. مؤرشف من الأصل في 2019-12-18. اطلع عليه بتاريخ 21 سبتمبر، 2018م.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة)،|موقع=تُجوهل (مساعدة)، ويحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ تبريبرات ثلاثية الابعاد للعلاقة القطبية بين نقطة وخط بالنسبة لقطاع مخروطي. د. حسن العيسوي (LINK) نسخة محفوظة 14 أغسطس 2019 على موقع واي باك مشين.
| مرافق زاوي في المشاريع الشقيقة: | |