مخروط

مخروط دائري قائم ومائل

في الرياضيات، المخروط هو مجسم ثلاثي الأبعاد ينتج من توصيل جميع نقاط منحنى مغلق بنقطة لا تنتمي إليه، ويسمى المنحنى الخط الدليلي والنقطة بـرأس المخروط ويسمى كل مستقيم يوصله بين الخط الدليلي والرأس بـراسم المخروط, ويعرف أيضا بأنه هو المجسم الناتج من تدوير مثلث قائم الزاوية حول أحد ضلعي الزاوية القائمة دورة كاملة. عندما يكون الخط الدليلي دائرة، يسمى المخروط مخروط دائري. وعندما تكون جميع الرواسم متساوية في الطول يسمى المخروط الدائري القائم. وإذا قطعنا المخروط الدائري القائم بمستوى لا يشمل رأسه، فإن المقطع الناتج يسمى القطع المخروطي.
وارتفاع المخروط هو المستقيم العمودي من قمة رأس المخروط إلى القاعدة، ويسمى أيضا طول المخروط.
إذا قيل مخروط بلا إضافات فإنه يكون المخروط الدائري.
يقع مركز ثقل المخروط ذو الكثافة المتجانسة على المحور، عند ربع المسافة من مركز ثقل القاعدة باتجاه القمة.

قوانين متعلقة بالمخروط

هذه القوانين حول المخروط الدائري

r : نصف قطر القاعدة.

h : ارتفاع المخروط.

A : مساحة القاعدة.

P : محيط القاعدة.

V : حجم المخروط.

g : هو طول الراسم في المخروط الدائري القائم.

مساحات

مساحة السطح الجانبي للمخروط الدائري القائم = $\frac{gP}{2}=\pi rg$

مساحة قاعدة المخروط = $\pi r^2$

عندما يُقطع مخروط دائري قائم بمستوى يوازي القاعدة فإنه ينتج مقطع بحيث: $\frac{a}{A}=\frac{k^2}{h^2}$

حيث a هو مساحة المقطع، و k هو بعد المقطع عن رأس المخروط.

الحجم

يتم إيجاد حجم المخروط الدائري القائم من خلال حساب ثلث مساحة القاعدة مضروبة في الارتفاع: $\frac{Ah}{3}$

يوضح الشكل كيفية توليد مخروط من خلال تدوير مثلث قائم الزاوية
الرسم السابق يوضح منحنى الدالة$d(x)=\frac{r}{h}x$

وقد تم اثباته باعتبار المخروط الدائري القائم مجسم دوراني ينتج عن تدوير الدالة $d(x)=\frac{r}{h}x$

وكأي مجسم دوراني فإن:

الحجم = المساحة تحت المنحنى تربيع مضروبا في ط

$V=\pi \underset{0}{\overset{h}{\int }}{\left(\frac{r}{h}x\right)}^{2}dx$ ايجاد المساحة عن طريق حساب التكامل

$V=\frac{\pi r^2}{h^2}\underset{0}{\overset{h}{\int }}{x}^{2}dx$ بتوزيع القوى على الضرب ثم إخراج الأعداد الثابتة.

$V=\frac{\pi r^2}{h^2}{\left[\frac{x^3}{3}\right]}_0^h$ حل التكامل

$V=\frac{\pi \times r^2\times h}{3}$ بحل التكامل ثم اختصار الارتفاع في البسط والمقام

$V=\frac{Ah}{3}$ وبما أن المساحة هي $A=\pi r^2$ وضعنا قيمتها.

وهو نفس القانون السابق.

المخروط الناقص

التسميات

• وفقًا لنوع المقطع القائم (straight cross-section) لمخروط ثنائي (quadric cone)، فإنه يصنف اهليجي، أو دائري أو مكافئي أو زائدي، عندما يكون مقطعه القائم قطع ناقص، أو دائرة أو قطع مكافئ، أو قطع زائد

المخروط المائل، عندما يكون محوره غير متعامد مع مستوى القاعدة. ولكن بالإشارة إلى المقطع القائم، فإنه لا يوجد مخاريط مائلة، بل جميعها قائمة.

• مخروط مبتور إذا تم قطع المخروط بمستو فإن الحيز بين مستوى القطع والقاعدة يسمى مخروط مبتور ويسمى أيضا جذع مخروطي.

أنواع القطوع المخروطية:
1. قطع مكافئ
2. دائرة وقطع ناقص
3. قطع زائد

بسط أو تطوير المخروط

• 
  بسط سطح مخروطي اهليجي

القطوع المخروطية

المقالة الرئيسية: قطوع مخروطية

عندما يقطع مستوى مخروط فإن ذلك يولد القطوع المخروطية وهي: القطع الزائد والقطع الناقص والقطع المكافئ.

يحدد السمك الثابت لمخروط إهليجي على مقطع دائري للمخروط نفسه

يحدد السمك الثابت لمخروط اهليجي على مقطع دائري للمخروط نفسه

معرض صور

• 
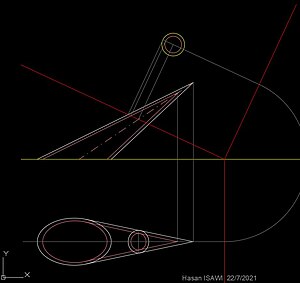
  إجراء هندسي لتحديد مقطع قائم لمخروط ثنائي بوضع عام . معلوم: القاعدة وقطب. الذي يمثل في هذه الحالة الأثر الأول لخط ينتمي إلى المستوى المقابل للخط القطبي بالنسبة للمخروط نفسه
• 
  مقاطع دائرية لمخروط اهليجي
• 
  توصيلات مماسية بين مخاريط دائرية قائمة

إنظر أيضا

• قطع مخروطي
• اسطوانة
• مجسم دوراني
• دليل (directrix)

المصادر

• كتاب الرياضيات الصف الثالث ثانوي الفصل الدراسي الثاني، طبعة 1431-1432 هـ، المملكة العربية السعودية.