|
تضامنًا مع حق الشعب الفلسطيني |
نظام كمي ذو حالتين
في ميكانيكا الكم ، نظام الحالتين (المعروف أيضا باسم نظام مستويين) هو نظام كمي يمكن أن يوجد في أي تراكب كمي من اثنين من الحالات الكمية .
فضاء هيلبرت يصف مثل هذا النظام ثنائي الأبعاد . لذلك، فإن الأساس الكامل الذي يمتد على المساحة يتكون من حالتين مستقلتين. يمكن أيضًا النظر إلى أي نظام قائم على حالتين على أنه كيوبت .
نظام الحالتين هو أبسط أنظمة الكم التي يمكن أن توجد، لأن ديناميكيات نظام الحالة الواحدة تافهة (أي لا توجد حالة أخرى يمكن أن يوجد فيها النظام). إن الإطار الرياضي المطلوب لتحليل أنظمة الحالتين هو المعادلات التفاضلية الخطية والجبر الخطي للمساحات ثنائية الأبعاد. ونتيجة لذلك، يمكن حل ديناميكيات نظام الحالتين بشكل تحليلي دون أي تقريب. السلوك العام للنظام هو أن سعة دالة الموجة تتأرجح بين الحالتين.
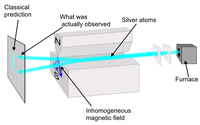
من الأمثلة المعروفة جيدًا لنظام الحالتين هو دوران جسيم spin-1/2 مثل الإلكترون، الذي يمكن أن يحتوي دورانه على قيم + ħ / 2 أو − ħ / 2 ، حيث ħ هو ثابت بلانك المختزل .
لا يمكن استخدام نظام الحالتين للامتصاص أو الانحلال، لأن مثل هذه العمليات تتطلب الاقتران بسلسلة متصلة. قد تنطوي مثل هذه العمليات على الانحلال الأسي للسعات، ولكن حلول نظام الحالتين تكون متذبذبة.
حلول تحليلية لطاقات الحالة الثابتة و اعتمادية الزمن
التمثيل
لنفترض أن الحالتين الأساسيتين المتاحتين للنظام هما و ، بشكل عام يمكن كتابة الحالة على أنها تراكب من هاتين الحالتين بسعات احتمالية :
إذا كانت الحالة الأساس غير طبيعية أي و هي دلتا كرونيكر ، لذا . يمكن اعتبار أرقام الإحداثيات في ثنائية الأبعاد فضاء هلبرت معقد. [1] وبالتالي ناقل الحالة المطابق للحالة يكون
وتتوافق حالات الأساس مع ناقلات الأساس، و .
إذا كانت الحالة و القاعدة من ال statevector هي وحدة، تكون .
ترتبط جميع الكميات الفيزيائية التي يمكن ملاحظتها، مثل الطاقة، بحكم العاملين . في حالة الطاقة والهاملتونيان المقابل، يعنى ، بمعنى آخر و حقيقية و . وبالتالي هذه العناصر المصفوفة الأربعة تنتج 2 2 مصفوفة محكمة .
- .
تنص معادلة شرودنجر المستقلة عن الزمن على ذلك ، واستبدال من حيث حالات الأساس، من كلا الجانبين من أو ينتج نظامًا من معادلتين خطيتين يمكن كتابتهما في شكل مصفوفة
هي 2 2 من مصفوفات ايجنفالوس ومشكلة المتجهات الذاتية . بسبب القيم الذاتية تكون حقيقية، أو العكس بالعكس، فالشرط أن تكون الطاقات حقيقية تعني ضمانية . تمثل المتجهات الذاتية الحالات الثابتة ، أي تلك التي لا يتغير فيها الحجم المطلق لمربعات اتساع الاحتمال مع مرور الوقت.
قيم ايجين من الهاميلتونيان
الشكل العام لـ 2 2 من مصفوفة الهرميت مثل هاميلتونيان لنظام الحالتين
أي و هي أعداد حقيقية مع وحدات الطاقة. يمكن العثور على مستويات الطاقة المسموح بها للنظام، وهي القيم الذاتية للمصفوفة هاميلتون، بالطريقة المعتادة.
يمكن أن تتحلل هذه المصفوفة على أنها
هنا، و هي أرقام حقيقية. المصفوفة هي 2 2 من مصفوفة الهوية والمصفوفات هي مصفوفات باولي . يبسط هذا التحلل تحليل النظام، خاصة في حالة مستقلة عن الوقت حيث قيم و هي ثوابت.
يمكن كتابة هاميلتونيان بشكل أكثر تعقيدًا على النحو التالي:
المتجه من و من . يبسط هذا التمثيل تحليل تطور الوقت للنظام ويسهل استخدامه مع التمثيلات المتخصصة الأخرى مثل المجال بلوتش .
إذا كان نظام هاميلتون مستقلا عن حالتي يتم تعريفه على النحو الوارد أعلاه، ثم يتم إعطاءه قيمه ذاتية من . من الواضح ان هو متوسط الطاقة للمستويين، ومعيار هو الانقسام بينهما. يشار إلى المتجهات الذاتية المقابلة و .
اعتمادية الوقت
نفترض الآن أن السعات الاحتمالية تعتمد على الوقت، على الرغم من أن حالات الأساس ليست كذلك. معادلات شرودنغر المعتمدة على الوقت ، و (استبدال من مرة أخرى ينتج زوج من المعادلات الخطية المزدوجة، ولكن هذه المرة هي المعادلات التفاضلية الجزئية من الدرجة الأولى: . إذا هو الوقت المستقل، هناك العديد من الأساليب، لإيجاد الاعتماد على الوقت ، مثل الأوضاع العادية . والنتيجة هي هكذا:
- .
أي هو statevector في . هنا يمكن العثور على أسية المصفوفة من توسع السلسلة. المصفوفة تسمى مصفوفة تطور الوقت (والتي تتضمن عناصر المصفوفة لعامل تطور الوقت المقابل ). هي وحدوية، وهذا يعني ان . يمكن أن يثبت ذلك هكذا:
أي .
عندما يغير المرء الأساس إلى المتجهات الذاتية لهاملتونيان، وبعبارة أخرى، إذا كان الأساس ينص على يتم اختيارهم ليكونوا المتجهات الذاتية بعد ذلك و وبالتالي فإن هاميلتونيون قطري، أي وهو من الشكل،
الآن عامل تطور الوقت الوحدوي يمكن رؤيته بسهولة من خلال:
ال يساهم فقط في المرحلة الإجمالية للمشغل ويمكن تجاهلها عادة لإنتاج عامل تطور زمني جديد لا يمكن تمييزه ماديًا عن المشغل الأصلي. علاوة على ذلك، يمكن إضافة أي اضطراب في النظام (والذي سيكون من نفس شكل هاميلتونيان) إلى النظام في الأساس الذاتي لهاملتونيان غير مضطرب وتحليله بنفس الطريقة المذكورة أعلاه. لذلك، لأي اضطراب، يمكن حل المتجهات الذاتية الجديدة للنظام المضطرب تمامًا، كما هو مذكور في المقدمة.
تركيبة رابي لاضطراب ثابت
افترض أن النظام يبدأ في إحدى حالات الأساس عند ، ، يكون التركيز باحتمال احتلال كل حالة أساس كدالة للوقت عندما يكون هو هاميلتوني مستقل عن الوقت.
احتمالية احتلال الحالة تكون . في حالة البداية، وما فوق، . بالتالي
ببساطة بسبب الحالة الأولية. التردد يسمى تردد رابي المعمم، يسمى التردد الرابي و يسمى detuning. عند detuning الصفري، ، أي أن هناك انحراف رابي من احتلال مضمون للحالة 1 ، إلى احتلال مضمون للحالة 2 ، والعودة إلى الحالة 1 وما إلى ذلك. . بينما يزداد ال بعيدًا عن الصفر، يزداد تواتر التقليب (إلى ) وينخفض التعة إلى .
انظر أيضًا دورة ربيع وتقريب الموجة الدوارة لهاميلتونيين يعتمد على الوقت الناجم عن موجات الضوء.
بعض أنظمة الحالتين المهمة
الاستباقية في المجال
لنأخذ حالة جسيم الدوران 1/2 في المجال المغناطيسي . تفاعل هاميلتونيان لهذا النظام هو
أي ان هو مقدار العزم المغناطيسي للجسيم، و هو ناقل مصفوفات باولي . حل معادلة شرودنجر المعتمدة على الوقت عائدة إلى هذا:
أي و . مادياً، يتوافق هذا مع ناقل بلوخ المتداول بتردد زاوي . بدون فقدان العمومية، افترض أن المجال هو نقاط موحدة في ، بحيث يتم إعطاء عامل تطور الوقت كـ
يمكن ملاحظة أن عامل تطور الوقت الذي يعمل على حالة الدوران العامة لجزيء الدوران 1/2 سيؤدي إلى استباقية حول المحور المحدد بواسطة المجال المغناطيسي المطبق (المكافئ الميكانيكي الكمومي لمسافة لارمور ) [2]
يمكن تطبيق الطريقة المذكورة أعلاه على تحليل أي نظام حالتين عام يتفاعل مع بعض المجالات (ما يعادل المجال المغناطيسي في الحالة السابقة) إذا تم التفاعل بواسطة اقتران مناسب مماثل للعزم المغناطيسي . يمكن اعتبار البادئة لناقل الحالة (التي لا تحتاج إلى الغزل المادي كما هو الحال في الحالة السابقة) على أنها البادئة لناقل الحالة على مجال بلوخ .
التمثيل في المجال بلوتش لمتجه الحالة سيكون ببساطة ناقل قيم التوقعات . كمثال، ضع في اعتبارك متجه الحالة الذي هو تراكب تطبيعي و ، أي ناقلات يمكن تمثيلها في ك
مكونات على المجال بلوخ ستكون ببساطة . هذا ناقل وحدة يبدأ بالإشارة و حولها بطريقة عسرى. بشكل عام، من خلال دوران حول أي ناقل حالة يمكن تمثيلها كـ مع معاملات حقيقية من و . مثل متجه الحالة هذا يتوافق مع ناقل بلوخ في : xz تصنع زاوية مع المحور- z . سوف يستمر هذا الناقل في الظهور ك . من الناحية النظرية، من خلال السماح للنظام بالتفاعل مع مجال اتجاه معين وقوة معينة لفترات دقيقة، من الممكن الحصول على أي اتجاه لمتجه بلوخ ، وهو ما يعادل الحصول على أي تراكب معقد. هذا هو الأساس للعديد من التقنيات بما في ذلك الحوسبة الكمومية والتصوير بالرنين المغناطيسي .
التطور في مجال اعتمادية الوقت: الرنين المغناطيسي النووي
الرنين المغناطيسي النووي (NMR) هو مثال مهم في ديناميكيات أنظمة الحاليتن لأنه يتضمن الحل الدقيق لهاملتوني يعتمد على الوقت. يتم تحقيق ظاهرة الرنين المغناطيسي النووي عن طريق وضع نواة في حقل ثابت قوي B 0 ("حقل التثبيت") ثم تطبيق مجال ضعيف وعرضي B 1 يتأرجح عند بعض الترددات الراديوية ω r . [3] بشكل صريح، ضع في اعتبارك جسيم الدوران 1/2 في حقل احتجاز وحقل الترددات المستعرضة B 1 يدوران في xy بطريقة عسرى () حول B 0 :
كما هو الحال في المبادرة الحرة، فإن هاميلتون هو ، وتطور ناقل الحالة يتم العثور عليها عن طريق حل معادلة شرودنجر المعتمدة على الوقت . بعد بعض التلاعب (كما هو موضح في القسم المنهار أدناه) ، يمكن إظهار أن معادلة شرودنغر تصبح
وفقًا للقسم السابق، فإن حل هذه المعادلة يحتوي على ناقل بلوخ مع تردد ضعف حجم المتجه. إذا كانت قوية بما فيه الكفاية، فإن بعض نسبة السبين سوف تشير مباشرة للأسفل قبل إدخال المجال الدوار. إذا تم اختيار التردد الزاوي للمجال المغناطيسي الدوار مثل هذا ، في الإطار الدوّار، سيبدأ متجه الحالة في الجوار مع التردد ، وبالتالي سوف تنقلب من أسفل إلى أعلى و تطلق الطاقة في شكل فوتونات قابلة للكشف [بحاجة لمصدر] . هذا هو الأساس الأساسي للرنين المغناطيسي النووي ، ومن الناحية العملية يتم تحقيقه عن طريق المسح الضوئي حتى يتم العثور على تردد الرنين عند هذه النقطة ستصدر العينة الضوء. يتم إجراء حسابات مماثلة في الفيزياء الذرية، وفي حالة عدم دوران المجال، ولكن تتأرجح بسعة معقدة، يتم استخدام تقريب الموجة الدوارة في استخلاص مثل هذه النتائج.
العلاقة مع معادلات بلوخ
يمكن اشتقاق معادلات بلوخ الضوئية لمجموعة من جزيئات الدوران 1/2 من معادلة شرودنجر المعتمدة على الوقت لنظام من مستويين. بدءا من هاميلتوني المذكور سابقا ، يمكن كتابتها في تدوين الجمع بعد إعادة ترتيبها
التضاعف في مصفوفة باولي والاقتران المترافق للوظيفة الموجية، وبالتالي توسيع ناتج حصيلة مصفوفات باولي، يكون هكذا:
إن إضافة هذه المعادلة إلى بديلها المتقارب يعطي جانبًا يساريًا من النموذج
والجهة اليمنى من النموذج
كما ذكرنا سابقًا، فإن القيمة المتوقعة لكل مصفوفة باولي هي مكون من متجه بلوخ ، . معادلة الجانبين الأيسر والأيمن وملاحظة هي النسبة المغنطيسية ، يعطي شكل آخر لمعادلات الحركة لمتجه بلوخ
حيث حقيقة تم استخدامها في شكل متجه و يمكن التعبير عن هذه المعادلات الثلاث من حيث المنتوج المتقاطع
كلاسيكيًا، تصف هذه المعادلة ديناميكيات الدوران في المجال المغناطيسي. يتكون المغناطيس المثالي من مجموعة من السبينات المتطابقة التي تعمل بشكل مستقل، وبالتالي التمغنط الكلي يتناسب مع ناقلات بلوخ . كل ما تبقى للحصول على الشكل النهائي لمعادلات بلوخ البصرية هو تضمين الظواهر.
كجانب نهائي، يمكن اشتقاق المعادلة أعلاه من خلال النظر في التطور الزمني لعامل الزخم الزاوي في تصوير هايزنبرغ .
، هذه المعادلة هي نفس المعادلة السابقة .
الصلاحية
أنظمة الحالتين هي أبسط أنظمة الكم غير العادية التي تحدث في الطبيعة، لكن طرق التحليل المذكورة أعلاه ليست صالحة فقط لأنظمة الحالتين البسيطة. بل يمكن معالجة أي نظام كمومي عام متعدد الحالات كنظام حالتين طالما أن النظام المرئي يركز على قيمتان ذاتيتان.
على سبيل المثال، قد يكون لجسيم الدوران 1/2 في الواقع درجات تحول إضافية أو حتى تناوب حر، لكنها ليست ذات صلة بالتحليل السابق. رياضيا، تتوافق درجات التناوب الحر المهملة مع انحطاط القيم الذاتية للدوران.
في حالة أخرى تكون فيها شكليات الحالتين الفعالة صحيحة عندما يكون للنظام قيد النظر مستويين يتم فصلهما عن النظام بشكل فعال. هذا هو الحال في تحليل الانبعاث العفوي أو المحفز للضوء بواسطة الذرات وتلك التي تشحن بالكيلوبتات .
في هذه الحالة، يجب أن يوضع في الاعتبار أن الاضطرابات (التفاعلات مع مجال خارجي) تقع في النطاق الصحيح ولا تتسبب في انتقالات إلى حالات أخرى غير تلك المهمة.
الأهمية وأمثلة أخرى
تعتبر شكليات الحالتين هي من أبسط التقنيات الرياضية المستخدمة لتحليل النظم الكمومية. يمكن استخدامها لتوضيح الظواهر الميكانيكية الكمومية الأساسية مثل التداخل الذي تظهره الجزيئات بحالات الاستقطاب للفوتون، [4] ولكن أيضًا ظواهر أكثر تعقيدًا مثل تذبذب النيوترينو أو تذبذب كي ميسون المحايد .
يمكن استخدام شكليات الحالتين لوصف الاختلاط البسيط للحالات، مما يؤدي إلى ظواهر مثل استقرار الرنين والتماثلات الأخرى المرتبطة بعبور المستوى .
هذه الظواهر لها تطبيق واسع في الكيمياء. يمكن تفسير الظواهر ذات التطبيقات الصناعية الهائلة مثل الماسر والليزر باستخدام شكليات الحالتين.
تشكل شكليات الحالتين أيضًا أساس الحوسبة الكمومية . كيوبيتس ، وهي اللبنات الأساسية لجهاز الكمبيوتر الكمومي . أي عملية حسابية كمومية هي عملية وحدوية تقوم بتدوير متجه الحالة على كرة بلوخ.
قراءة متعمقة
- طريقة ممتازة لشكل الحالتين وتطبيقها على جميع التطبيقات تقريبًا المذكورة في هذه المقالة في المجلد الثالث من محاضرات فينمان في الفيزياء .
- المجموعة التالية من ملاحظات المحاضرة تغطي الرياضيات اللازمة وتعالج أيضًا بعض الأمثلة ببعض التفاصيل:
- من دورة ميكانيكا الكم II المقدمة في معهد ماساتشوستس للتكنولوجيا ، http://web.mit.edu/8.05/handouts/Twostates_03.pdf
- من نفس الدورة التي تتعامل مع تذبذب الجسيمات المحايدة، http://web.mit.edu/8.05/handouts/nukaon_07.pdf
- من دورة ميكانيكا الكم التي عرضت في TIFR ، http://theory.tifr.res.in/~sgupta/courses/qm2013/hand4.pdf و تغطي الرياضيات الأساسية
- http://theory.tifr.res.in/~sgupta/courses/qm2013/hand5.pdf ؛ من نفس المقرر يتعامل مع بعض أنظمة الحالتين المادية والجوانب الهامة الأخرى من الشكليات
- يتم الحساب في القسم الأولي بطريقة مماثلة لهذه الملاحظات http://www.math.columbia.edu/~woit/QM/qubit.pdf ، وهي من دورة ميكانيكا الكم لعلماء الرياضيات المقدمة في جامعة كولومبيا .
- نسخة كتاب منها ؛ http://www.math.columbia.edu/~woit/QM/qmbook.pdf
المراجع
| نظام كمي ذو حالتين في المشاريع الشقيقة: | |