|
تضامنًا مع حق الشعب الفلسطيني |
نموذج الكوارك
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. (يناير 2022) |
نموذج الكوارك في الفيزياء هو عبارة عن نظام لتصنيف هادرونات من حيث كوارك المكافئ— حيث يعطي الكوارك وضديده رقم كم للهادرون. ولتلك الأرقام الكمية أسماء تحدد بها الهادرونات، وهي من نمطين. مجموعة تأتي من تناظر بوانكاريه— JPC حيث J, P وC ترمز إلى الزخم الزاوي الإجمالي وتناظر التكافؤ وتناظر الشحنة على التوالي. والباقي هو نكهات أعداد الكم مثل لف نظائري والغرابة والسحر وهكذا. ويعتبر نموذج كوارك متابعة لنظام تصنيف طريق الثمان لفات.
تحدد الكواركات كلها رقم باريون ل1⁄3. فلدى الكوارك العلوي والساحر والقمة شحنة كهربائية تعادل +2⁄3، بينما الكوارك السفلي والغريب والقعري لديها شحنة كهربائية −1⁄3. أما ضديد الكواركات فلديها رقم كمي معاكس. ولدى الكوارك أيضا دوران مغزلي -1⁄2 من الجسيمات، ويعني بأنها فرميونات.
تتكون الميزونات من زوج كوارك مكافئ-ضديد كوارك (مما يعني أن لديها رقم باريون = 0)، بينما تتكون الباريونات من ثلاث كواركات (مما يعني أن رقم الباريون لديها= 1). ويناقش المقال هنا نموذج الكوارك لنكهات الكوارك العلوية والسفلية والغريبة. هناك تعميمات لأعداد أكبر من النكهات.

البداية
في ظل التطوير لنظام تصنيف الهادرونات أضحت هناك أسئلة ساخنة بعد كشف أساليب فنية تجريبية جديدة، فأصبح واضحا أن لا يمكن أن تكون جميعها أولية. فقد أدت تلك الاكتشافات إلى فولفغانغ باولي بأن يصرخ قائلا:«ماكنت أتوقع ذلك، وإلا كنت سأصبح عالم نبات» ولكن لويس ألفاريز الذي أخذ بها جائزة نوبل في فيزياء الجسيمات التجريبية كان في طليعة تلك التطورات. هناك العديد من المقترحات المبكرة ولكن لم تكن لها القدرة على الشرح الكامل لتلك المعطيات مثل مقترح سويجي ساكوتا. ثم أتت النسخ المطورة من مويونج هان ويويتشيرو نامبو التي أضحت أنه لايمكن الاعتماد عليها بعد ذلك. فتم تطوير صيغة جيلمان-نشيجيما على نحو تكوين جديد ومطور لنموذج الكوارك بين موري جيلمان وكازهيكو نشيجيما. ثم تلقى هذا النموذج دعم ومساهمة من يوفال نعمان وجورج سويج. فالذي تنبأ بهذا النموذج هو لف 3⁄2 باريون
Ω−
وهو أحد الحالات البسيطة، واكتشفه جيلمان عن طريق تجربة في مختبر BNL واستحق جائزة نوبل على عمله هذا على تطوير نموذج الكوارك.
الميزونات
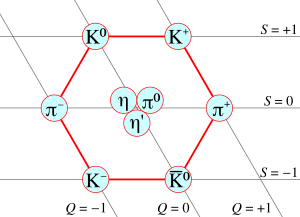

سمي تشكيل طريق الثمان لفات بعد الأمر التالي. إذا اخذنا 3 نكهات من الكواركات، ستكون الكواركات في التمثيل الأساسي، 3 (وتسمى ثلاثي) من نكهة SU3. ويكون ضديد الكوارك في التمثيل المعقد المقارن 3. وتصنع الحالات التسع (تساعي) من زوج يمكن أن يتحلل إلى التمثيل الكاذب 1 ويسمى المفرد، والتمثيل المشترك 8 (يسمى ثُماني). والترميز لهذا التحلل هو
- .
فالشكل الأول يظهر تطبيق تحلل الميزونات. فإذا كان تناظر النكهة متكاملا، فستصبح كل الميزونات التسع متساوية الكتلة. ويشمل المحتوى المادي للنظرية مراعاة كسر التناظر الناتج من اختلاف كتل الكواركات وأيضا مراعاة الخلط بين التعدد المختلف (مثل الثُماني والمفرد). فالصدع ما بين
η
و
η′
هو أكبر من استيعاب نموذج الكوارك.
الميزونات هي هادرونات لها صفر رقم باريون. فإن كان زوج الكوارك-ضديد الكوارك في حالة عزم زاوي مداري L ولهما لف مغزلي S، فإنه:
- |L − S| ≤ J ≤ L + S، حيث S =0 أو 1،
- P = (−1)L + 1، حيث 1 في الأس نشأ من جوهر التكافؤ لزوج الكوارك-ضديد الكوارك.
- C = (−1)L + S للميزونات التي ليس لها نكهة. أما الميزونات ذات النكهة فلها قيمة غير محددة لC
- في اللف النظائري I = حالتي 1 و 0، أحدهما يمكنه تحديد رقم كمي مضاعف جديد ويسمى تكافؤ-G مثل هذه G = (−1)I + L + S.
- إن كانت P =(−1)J فإنه يترتب على ذلك أن S =1، بالتالي PC =1. تسمى الحالات مع تلك الأرقام الكمية بحالات تكافؤ طبيعي، بينما تسمى حالات الأرقام الكم الأخرى بالشاذة (مثل حالة JPC = 0−−)
باريونات


انظر أيضًا
- جسيم دون ذري
- هادرونات، باريونات, ميزونات كواركات
- هادرون شاذ: ميزون شاذ باريون شاذ
- ديناميكا لونية كمومية، نكهة، QCD vacuum
مصادر ووصلات خارجية
- J.R. Christman (2001). "SU(3) and the quark model" (PDF). Project PHYSNET. جامعة ميشيغان. MISN-0-282. مؤرشف من الأصل (PDF) في 2006-02-21. اطلع عليه بتاريخ 2009-07-24.
- S. Eidelman et al. (Particle Data Group (2004). "Review of Particle Physics" (PDF). Physics Letters B. ج. 592: 1. DOI:10.1016/j.physletb.2004.06.001. مؤرشف من الأصل (PDF) في 2020-11-29.
- H. Georgi (1999). Lie algebras in particle physics. Perseus Books. ISBN:0-7382-0233-9.
- J.J.J. Kokkedee (1969). The quark model. W. A. Benjamin. (أمازون B001RAVDIA).
