|
تضامنًا مع حق الشعب الفلسطيني |
تواز (هندسة)
| مسافات رياضية | |
|---|---|
| دوال | |
| دالة مسافة | دالة مسافة متجهة |
| مسافة شبشفية | مسافة إقليدية |
| مسافة هاوسدورف | مسافة سيارة الأجرة |
| مسافة | |
| مسافات بين كائنات رياضية | |
| بين نقطة وخط | بين نقطتين |
| بين نقطة ومستوى | بين خطين متوازيين |
| بين خطين متخالفين | |
| حالات وعلاقات الكائنات الهندسية فيما بينها | |
|---|---|
| تسامُتٌ | تلاقٍ |
| توازٍ | تعامد |
| تنصيف | انطباقٌ |
| دَائريَّةٌ | تماس |

| |
| السعي نحو اللانهاية | انعدامٌ |
| مُخالَفَةٌ | اشتراك في مستوى |

في الهندسة الرياضية، يعبر التوازي عن علاقة ثنائية بين كائنين هندسيين مثل خطين مستقيمين أو مستويين، وتشترط هذه العلاقة استحالة التقاء هذين الكائنين في جميع نقاط الفضاء.[1] يرمز لعملية التوازي بين خطين a b بهذة الطريقة .
التوازي في الهندسة الوصفية
حالات التوازي في الهندسة الوصفية، يمكن ان تتحقق بين الكيانات الأساسية التالية:
- بين خطين مستقيمين
- بين خط وسطح مستوي
- بين سطحين مستويين
التوازي بين خطين مستقيمين
التوازي بين الخطوط في علم الهندسة الوصفية يتحقق في مختلف أساليب التمثيل على النحو التالي :

في الإسقاط الموازي
في الإسقاط الموازي (طريقة مونج الاكسنومتري), خطين يكونان متوازيين عند وجود على الأقل إسقاطين متوازيين على التوالي لبعضهما البعض، مثلاً, في طريقة مونج, خطين r و s يكونان متوازيين عندما الإسقاط الأول r1 للخط r يكون موازي للإسقاط الأول s1 للخط s والإسقاطات الثانية r2 s2 تكون متوازية (رسم2).
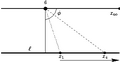
في الإسقاط المركزي
في الإسقاط المركزي, (المنظور) الإسقاطات المركزية لخطوط متوازية لبعضهما البعض تتمثل في خطوط تلتقي في نفس نقطة التلاشي. ينبغي الاخذ في الاعتبار انة عندما تكون الخطوط موازية أيضاً لمستوى الإسقاط، نقطة التلاشي تكون لانهائية.
التوازي بين خط ومستوى
خط r يوازي مستوى α (الفا), عندما r يوازي خط s ينتمي إلى الفا. هذا الشرط يتحقق في أساليب التمثيل الهندسية المختلفة (طريقة مونج, أكسونومتري ومنظور) على النحو التالي :
في الإسقاط الموازي (طريقة مونج، أكسونومتري)
خط r يوازي مستوى الفا، عندما يمكن ايجاد خط s ينتمي إلى الفا ويوازي الخط r، وهذا يعني انة يجب أن يكون هناك شرطين:
- شرط الانتماء للخط s إلى المستوى الفا، وهذا يتحقق عندما يوجد هناك على الاقل نقطين من s ينتميان إلى خطين معلومين من الفا.
- شرط التوازي بين الخطين r و s, وهذا يتحقق عندما يوجد هناك على الاقل إسقاطين 's و"s للخط s يوازيان إسقاطين 'r و"r للخط r
في الإسقاط المنظوري
خط r يوازي مستوى الفا، عندما الخطين r و s لهما نفس نقطة التلاشي والتي تنتمي إلى خط تلاشي الفا.
التوازي بين سطحين مستويين
مستويين ألفا α وبيتا β يكونوا متوازيين إذا وفقط إذا على كل واحد منهما خطين موازيين للمستوى الأخر.
في طريقة مونج
في طريقة مونج، مستويين ألفا وبيتا يكونين متوازيين، إذا كان الإسقاط المونجي (a1, a2 و b1, b2) لخطين a b, ينتميان إلى واحد منهما(مثلاً لالفا) موازي للإسقاط المونجي (d1, d2 و c1, c2) لخطين c d ينتميان للمستوى الثاني بيتا.
مثلاً, إذا كان لدينا مستويان α β في وضع عام، وأردنا التحقق ما إذا كان هناك توازي بينهما، نتصرف على النحو التالي:
- نجد أثار (t"α, t'α) للمستوى α
- نجد أثار (t"β, t'β) للمستوى الأخر β
- إذا كان هناك توازي بين الآثار المجانسة لتلك المستويات α β, يعني ان α β متوازيان، وإلا فهما متقاطعان.
المستقيمات المتوازية وازواج الزوايا
2.1. نظرية الزاويتين المتبادلتين داخليا:إذا قطع قاطع مستقيمين متوازيين فان كل زاويتين متبادلتين داخليا متطابقتان
2.2. نظرية الزاويتين المتحالفتين:إذا قطع قاطع مستقيمين متوازيين فان كل زاوتيتين منحالفتين متكاملتان
2.3. نظرية الزاويتين المتبادلتين خارجيا:إذا قطع قاطع مستقيمين متوازيين فان كل زاويتين متبادلتين خارجيأ متطابقتان
2.4. نظرية القاطع العمودي:إذا كان مستقيم عموديا على أحد مستقيمين متوازيين في مستوى فانه يكون عموديا على المستقيم لاخر
التواز بين سطوح دويرية
بالنظر إلى حقيقة أن جميع الإجراءات الهندسية المستخدمة لحل مشكلة التوازي بين دويريات مخروطية تعتمد على مفاهيم التقابل نفسها، فإن استخدام مصطلح واحد: التوازي الإسقاطي(Projective offst) ، يصبح ضروري للإشارة إلى جميع حالات التوازي سواء كانت ثابتة أو متغيرة بشكل منتظم.[2]
المنحنى المواز لقطع ناقص
المنحنى المواز لقطع ناقص يسمى منحنى حلقي (بالايطالية Toroide)، لأنها تشبه الكفاف الظاهر لسطح حلقي مسقط من مركز لانهائي.[3]
معرض صور
-
اسقاط موازي لدويرية من الكرات
مراجع
- ^ "Mathematical Operators – Unicode Consortium" (PDF). مؤرشف من الأصل (PDF) في 2018-06-12. اطلع عليه بتاريخ 2013-04-21.
- ^ Geometric Loci نسخة محفوظة 16 مايو 2019 على موقع واي باك مشين.
- ^ Volume II: curve trascendenti -curve dedotte da altre نسخة محفوظة 20 سبتمبر 2021 على موقع واي باك مشين.
وصلات خارجية
| جزء من سلسلة مقالات حول |
| الهندسة الرياضية |
|---|
 |
| علماء الهندسة |
| بوابة هندسة رياضية |