مساحة الدائرة

في الهندسة الرياضية، تعرف المساحة الموجودة داخل دائرة ما بمساحة الدائرة، ويمكن حسابها باستخدام المعادلة الرياضية: πr². حيث يمثل r نصف قطر الدائرة، أما الحرف اليوناني π فيمثل النسبة الثابتة لمحيط أي دائرة إلى قطرها، ويساوي تقريبًا 3,14159.

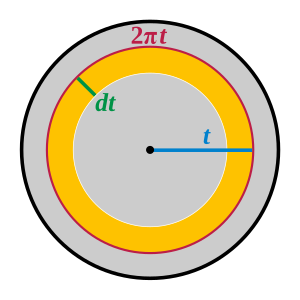
أحد الأساليب لاشتقاق هذه الصيغة والتي تصورها أرخميدس في الأصل، يستلزم النظر إلى الدائرة باعتبارها نهاية سلسلة من المضلعات المنتظمة مع عدد متزايد من الجوانب. يمكن حساب مساحة المضلع المنتظم بضرب نصف محيطه في المسافة من مركزه إلى أضلاعه. ولأن التسلسل يميل إلى أن يشكل دائرة، فإن الصيغة المقابلة – أن المساحة تساوي نصف المحيط في نصف القطر – هي: A = 1/2 × 2πr × r تمثل مساحة الدائرة.

التسمية

على الرغم من أنه يشار إليها غالبًا باسم مساحة الدائرة في السياقات غير الرسمية، إلا أن مصطلح القرص يشير بدقة إلى المنطقة الداخلية للدائرة، في حين أن الدائرة مخصصة للحدود فقط، وهو منحنى ولا يغطي أي مساحة بحد ذاتها. ولذلك، فإن مساحة القرص هي العبارة الأكثر دقة للمنطقة المحاطة بدائرة.

تاريخ

تستخدم الرياضيات المعاصرة حساب التفاضل والتكامل ونظيره الأكثر تقدمًا، وهو التحليل الحقيقي، لتحديد مساحة القرص. ومع ذلك، تمت دراسة مساحة القرص من قبل اليونانيين القدماء. في القرن الخامس قبل الميلاد وجد إيودوكسوس من كنيدوس أن مساحة القرص تتناسب مع مربع نصف قطره. استخدم أرخميدس في عمله "قياس الدائرة" أدوات الهندسة الإقليدية ليثبت أن المساحة داخل الدائرة تساوي مساحة المثلث القائم الذي قاعدته طول محيط الدائرة وارتفاعه يساوي نصف قطر الدائرة، ونظرًا لأن طول المحيط هو 2πr، ومساحة المثلث هي نصف القاعدة مضروبة في الارتفاع، فإن هذا الحساب يعطي المعادلة الرياضية (π r²) والتي تمكن من حساب مساحة لقرص. قبل أرخميدس، كان أبقراط الخيوسي أول من أثبت أن مساحة القرص تتناسب مع مربع قطره، كجزء من عمله على تربيع هلال أبقراط، لكنه لم يحدد ثابت التناسب.

استعمال متعددي الأضلاع

مساحة مضلع منتظم تساوي نصف محيطه مضروبا في المسافة الفاصلة بين مركز المضلع وأحدٍ من أضلاعه. كلما كبُر عدد أضلاع مضلع منتظم، كلما اقترب المضلع المنتظم من الدائرة التي تضمه، وكلما اقتربت هذه المسافة من شعاع الدائرة. هذا الأمر يؤكد أن مساحة القرص تساوي نصف محيط الدائرة مضروبا في شعاعها.

برهان أرخميدس

ليس أكبر من

دائرة ومربع وثماني أضلاع. الدائرة محيطة بهما مبينة الفرق في المساحة باللون الأصفر.

انظر إلى دائرة محيطة.

$\begin{array}{ll}E& =C-T\\ & >G_n\\ P_n& =C-G_n\\ & >C-E\\ P_n& >T\end{array}$

ليس أصغر من

دائرة ومربع وثماني أضلاع. الدائرة محاطة بهما مبينة الفرق في المساحة باللون الأصفر.

$\begin{array}{ll}D& =T-C\\ & >G_n\\ P_n& =C+G_n\\ & <C+D\\ P_n& <T\end{array}$

براهين عصرية

برهان البصلة

مساحة القرص بواسطة تكامل الحلقات

انظر بصل.

$\begin{array}{ll}\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}(r)& =\underset{0}{\overset{r}{\int }}2\pi tdt\\ & ={[(2\pi )\frac{t^2}{2}]}_{t=0}^r\\ & =\pi r^2.\end{array}$

طريقة المثلث

نشرت الدائرة من أجل تكوين مثلث.

الصيغة المستعملة من أجل حساب مساحة المثلث.

$\begin{array}{ll}Area& =\frac{1}{2}*base*height\\ & =\frac{1}{2}*2\pi r*r\\ & =\pi r^2\end{array}$

طريقة نصف الدائرة

نصف دائرة شعاعها r

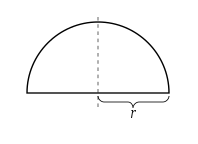
باستعمال تعريف التكامل ذاته، يمكن أن يُستنتج أن مساحة نصف الدائرة تساوي

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-x^2}dx$

باستعمال تعويض مثلثي يتمثل في وضع $x=r\sin \theta$، نجد أن $dx=r\cos \theta d\theta .$

$=\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\sqrt{r^2(1-{\sin }^2\theta )}\cdot r\cos \theta d\theta$

$=2r^2\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^2\theta d\theta$

$=\frac{\pi r^2}{2}.$

التقريب بالرمي بالنبال

تحديد مساحة الدائرة باستعمال طريقة تكامل مونت كارلو. التقدير ب 900 عينة يعطي 4×⁷⁰⁹⁄₉₀₀ = 3.15111...

انظر طريقة مونت كارلو.

وصلات خارجية

• مساحة القرص مع رسوم متحركة