|
تضامنًا مع حق الشعب الفلسطيني |
نسبة الاضمحلال
| الميكانيكا الكلاسيكية |
|---|
| تاريخ الميكانيكا الكلاسيكية |
| بوابة الفيزياء |
الإضمحلال أو التوهين (بالإنجليزية: Damping)؛ تأثير يحدث على أو ضمن نظام متذبذب يعمل على منع وتقييد ومقاومة حركته، فيزيائياً يحدث الإضمحلال نتيجة تبدد جزء من طاقة الحركة المختزنة في النظام بفعل وجود عرقلة لهذا التذبذب وكأمثلة على أنواع العرقلة،[1] لزوجة الوسط المحيط بالمهتز الميكانيكي، والمقاومة في المذبذبات الألكترونية والإمتصاص والحيود في المذبذبات البصرية، بينما الإضحملال الذي لا يعتمد على فقدان الطاقة يمكن أن يكون مهماً في الأنظمة البيولوجية و ديناميكا الدراجات [English].[2]
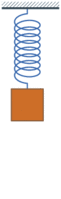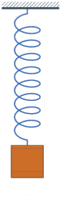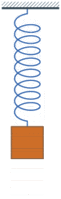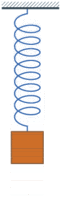
يمكن تعريف نسبة الإضمحلال بأنها مقياس يصف سرعة إضمحلال المهتزات بين ذبذبتين متعاقبتين وهي قيمة بدون وحدة تصف حالة إهتزاز نظام بعد بدء الحركة، حيث أن الكثير من الأنظمة تسلك سلوك مهتز عند إزاحتها عن موضع إتزانها، مثلاً الحركة الإهتزازية العمودية إلى الأعلى والأسفل لكتلة معلقة بنابض عند سحبها عن موضع إتزانها ثم تحريرها، يهدف النظام للعودة إلى موضع إستقراره لكنه في كل ذبذبة يتجاوز نقطة الإستقرار بفعل إستمرارية الحركة، خسارة طاقة النظام في كل ذبذبة تؤدي إلى إخماد الحركة بشكل تدريجي حتى تصل إلى الصفر إو إلى قيمتها الصغرى.
تمثل نسبة الإضمحلال صفة مميزة للنظام ويشار لها بالحرف (زيتا: )، ولها قيم بين:
() للنظام غير المضمحل، () للنظام المضمحل، () للنظام الحرج، () فوق المضمحل.
سلوك الأنظمة المهتزة غالباً ما يكون مهماً في عدد كبير من التخصصات مثل هندسة التحكم، والهندسة الكيميائية، والهندسة الميكانيكية، الهندسة الإنشائية، والهندسة الكهربائية، الكمية الفيزيائية التي تكون تحت الدراسة تختلف حسب التخصصات من الممكن أن تكون تأرجح لمبنى مرتفع أو سرعة دوران محرك كهربائي لهذا من السهل والمفيد استعمال التعبير الخالي من الوحدات في وصف الظواهر الإضمحلال لمختلف الظواهر.
حالات الإضمحلال
على سبيل المثال لنظام يتكون من كتلة معلقة بنابض شاقولي:
- في حالة إنعدام الخسار بالطاقة، يمكن للكتلة التأرجح إلى المالانهاية حيث أن سعة الإهتزاز أو إزاحتها عن موضع الإستقرار تكون متساوية بين كل ذبذبتين متعاقبتين، تسمى هذه الحالة (حركة غير مضمحلة).
- إذا كان للنظام خسارة طاقة عالية جداً، مثلاً عند إزاحة الكتلة عن موضع إستقرارها في سائل لزج، ستعود الكتلة إلى موضع إتزانها ببطء، وهذه الحالة تسمى (حركة فوق مضمحلة).
- بشكل عام، الكتلة ستتجاوز موضع إتزانها لكنها ستفقد مقداراً من الطاقة عند كل ذبذبة مما يجعل إزاحتها عن موضع إتزانها عند الذبذبة التالية أقل من سابقتها ويستمر فقدان الطاقة حتى تختفي الحركة وتستقر الكتلة عند موضع الإتزان، وهذه الحالة تسمى (حركة مضمحلة).
- مابين حالة فوق الإضمحلال والحركة المضمحلة يوجد مستوى معين حيث يفشل النظام في إنجاز ذبذبة واحدة وتعود الكتلة مباشرةً إلى موضع الإستقرار، تسمى هذه الحركة (الإضمحلال الحرج)، الفرق الرئيسي بين الإضمحلال الحرج وفوق الإضمحلال هو أن النظام في الحالة فوق الإضمحلال سيعود إلى نقطة إستقراره في أقل فترة زمنية ممكنة.
-
حركة توافقية بسيطة، من دون إضمحلال ().
-
حركة توافقية مضمحلة، قيمة نسبة الإضمحلال ().
التعريف

يرمز إلى نسبة الإضمحلال عادة بالرمز (زيتا: )،[3] وهي مقدار مهم خاصة في نظرية التحكم، ودراسة المهتز التوافقي.
تعبر نسبة الإضمحلال رياضياً عن مستوى الإضمحلال في النظام نسبةً إلى الإضمحلال الحرج، لمهتز توافقي كتلته ()، ومعامل الإضمحلال ()، وثابت نابض ()، يمكن تعريف نسبة الإضمحلال بأنها النسبة بين معامل الإضمحلال في المعادلة التفاضلية للنظام على معامل الإضمحلال الحرج، كما يلي:
ومعادلة الحركة للنظام تعطى بالصيغة التالية:
ومعامل الإضمحلال الحرج يعطى بالشكل:
أو
حيث أن: يمثل التردد الطبيعي للنظام المهتز.
لكون نسبة الإضمحلال هي نسبة بين مقدارين متماثلين بالوحدة فهي معامل خالي من الوحدات.
الاشتقاق
باستخدام التردد الطبيعي لمهتز توافقي () وتعريف نسبة الإضمحلال أعلاه يمكننا إعادة كتابة المعادلة بالشكل التالي:
الحل التقريبي لهذه المعادلة يعطى بالشكل:
حيث أن و هما ثوابت معقدة، وقيمة المناسبة له تعطى بالشكل:
تعطي هذه القيمة حلان مناسبان للمعادلة، يمكن ربطهما معاً لتكوين عدة حلول عامة حقيقية، لعدة حالات من الإضمحلال كما يأتي:
غير مضمحل
في هذه الحالة تكون () والتي تصف حالة مذبذب توافقي بسيط عديم الإضمحلال، وهنا يكون حل المعادلة .
حالة الإضمحلال
إذا كانت () هي زوج من القيم المعقدة، سيؤدي كل حد معقد منهم إلى حل بإضمحلال أُسي بالشكل . هذه الحالة تحدث بين () وتشير إلى حالة الإضمحلال.
فوق الإضمحلال
إذا كانت () زوج من القيم الحقيقية، عندها الحل عندها سيكون مجموع حدين من الإضمحلال الأسي بدون تذبذب، هذه الحالة تحدث عند () وتشير إلى حالة فوق الإضمحلال.
إضمحلال حرج
هذه الحالة عند قيمة ()، هي الحد الفاصل بين الحالة المضمحلة وفوق الإضمحلال، ويشيار إليها بالإضمحلال الحرج، عادة ما تكون مهمة في كثير من الحالات التي تتطلب تصميم هندسي معتمد على مهتز توافقي (مثلاً، ميكانيك لإغلاق الباب).
عامل النوعية ومعدل الإضمحلال
يمكن التعبير عن علاقة عامل النوعية أو إختصاراً (عامل )، بنسبة الإضمحلال، ومعدل الإضمحلال () بالمعادلة التالية:[4]
عندما يكون النظام مضمحلاً ()، يكون له قطبان معقدان مترافقان كل منهما يملك جزء حقيقي من ، حيث أن المعامل () يمثل معدل الإضمحلال الأسي للمهتزات، علاقته طردية مع نسبة الإضمحلال أي كلما كانت نسبة الإضمحلال أوطأ يكون معدل الإضمحلال أصغر، أي سيبقى النظام يهتز لوقت أطول،[5] على سبيل المثال: الشوكة الرنانة عالية الجودة ذات نسبة الإضمحلال المنخفضة جداً، يدوم إهتزازها لفترة طويلة، وتضمحل بشكل بطيء جداً بعد طرقها بمطرقة.
التناقص اللوغاريتمي
للمهتزات المضمحلة، يمكن ربط نسبة الإضمحلال بالتناقص اللوغاريتمي [English] الذي يرمز له () عن طريق العلاقة:
حيث أن:
() و () هما سِعات الإهتزاز عند قمتين متتاليتين لحركة مضمحلة.
تجاوز الحد المئوي
في نظرية التحكم، تجاوز الحد يشير إلى أن الخرج الناتج يتجاوز قيمته النهائية المستقرة ويتذبذب حولها قبل وصوله إلى الإستقرار،[6] ولإدخال درجي، تكون قيمة تجاور الحد المئوي إختصاراً (PO) مساوية للقيمة العظمى ناقصاً قيمة الخطوة مقسومة على قيمة الخطوة، في حالة قيمة عظمى مساوية لـ () يمكن أن يعطى مقدار تجاوز الحد المئوي بدلالة نسبة الإضمحلال () كما يلي:
وعلى العكس من ذلك، يمكن أن نحصل على نسبة الإضمحلال بدلالة قيمة تجاوز الحد المئوي:
المراجع
- ^ An introduction to mechanical vibrations. New York,: Wiley. [1971]. ISBN:0-471-82091-1. OCLC:199963. مؤرشف من الأصل في 4 أغسطس 2020.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ=(مساعدة)صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Meijaard، J.p؛ Papadopoulos، Jim M؛ Ruina، Andy؛ Schwab، A.l (8 أغسطس 2007). "Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. ج. 463 ع. 2084: 1955–1982. DOI:10.1098/rspa.2007.1857. مؤرشف من الأصل في 2020-07-29.
- ^ Introduction to mechatronics and measurement systems (ط. 3rd ed). Dubuque, IA: McGraw-Hill. 2007. ISBN:978-0-07-296305-2. OCLC:61309313. مؤرشف من الأصل في 2020-08-04.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (مساعدة) - ^ Circuits, signals, and systems. Cambridge, Mass.: MIT Press. 1986. ISBN:0-262-19229-2. OCLC:11784016. مؤرشف من الأصل في 2020-08-04.
- ^ Process control engineering : a textbook for chemical, mechanical and electrical engineers. Yverdon, Switzerland: Gordon and Breach Science Publishers. 1993. ISBN:2-88124-628-1. OCLC:28854255. مؤرشف من الأصل في 2020-08-04.
- ^ Automatic control systems (ط. 8th ed). New York: John Wiley & Sons. 2003. ISBN:0-471-13476-7. OCLC:50737026. مؤرشف من الأصل في 2020-08-04.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (مساعدة)