|
تضامنًا مع حق الشعب الفلسطيني |
قرصة بلازما
القرصة (أو قرصة بينيت [2] (المسماة عن ويلارد هاريسون بينيت ) ، قرصة كهرومغناطيسية ، [3] أو قرصة مغناطيسية ، [4] تأثير القرصة ، [5] أو قرصة بلازما .[6] ) هي ضغط موصل وتري كهربائي بواسطة قوى مغناطيسية ، أو جهاز يقوم بتلك العملية. عادة ما يكون الموصل عبارة عن بلازما ، ولكن يمكن أن يكون أيضًا معدنًا صلبًا أو سائلًا. كانت القرصات هي النوع الأول من الأجهزة المستخدمة للتجارب في طاقة الاندماج النووي المنضبط .[7]
تحدث القرصات بشكل طبيعي في التفريغ الكهربائي في الصواعق ، [8] الشفق الكوكبي ، [9] الصفائح التي تمر فيها تيار كهربي ، [10] والتوهجات الشمسية .[11]
الآلية الأساسية
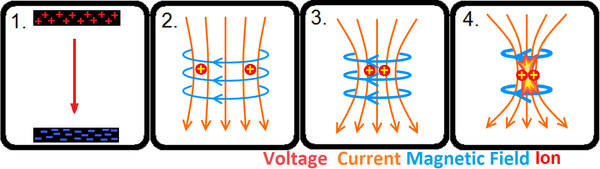
الأنواع


توجد القرصات في الطبيعة وفي المختبرات. القرصات تختلف في هندستها وقوى التشغيل.[12] وهي تشمل :
- غير متحكم فيه - في أي وقت يتحرك فيه تيار كهربائي بكميات كبيرة (مثل البرق ، والأقواس الكهربية ، والشرر ، والتفريغ) ، يمكن للقوة المغناطيسية أن تسحب البلازما وتكثيفها. وقد يكون هذا غير كافٍ للاندماج.
- قرصة في مساحة - هو تأثير فيزيائي فلكي ، ينشأ من طبقة مستوية واسعة من الجسيمات المشحونة.[13]
- القرصة على شكل Z - يمر التيار في محور أو عبر جدران أسطوانة بينما يكون المجال المغناطيسي سمتياً
- قرصة ثيتا - يمر المجال المغناطيسي خلال محور أسطوانة، بينما يكون المجال الكهربائي في اتجاه السمتي (ويسمى أيضًا ثيتاترون [14] )
- قرصة لولبية - مجموعة من قرصات Z و قرصات ثيتا [15] (تسمى أيضًا قرصة Z المستقرة أو قرصة θ-Z) [16][17]
- قرصة المجال المعكوسة أو القرصة الحلقية - هذه هي قرصة Z مرتبة في شكل طارة . تحتوي البلازما على مجال مغناطيسي داخلي. مع زيادة المسافة من مركز هذه الحلقة يعكس المجال المغناطيسي اتجاهه.
- القرص العكسي - مفهوم الاندماج المبكر ، يتكون هذا الجهاز من قضيب محاط بالبلازما. يسير التيار عبر البلازما ويعود على طول القضيب المركزي.[18] كانت هذه الهندسة مختلفة قليلاً عن z-pinch حيث كان الموصل في المركز ، وليس الجوانب.
- قرصة أسطوانية
- تأثير قرصة متعامدة
- قرصة المستودع - قرصة تحدث داخل بلازما توكاماك ، عندما تتكثف الجزيئات الموجودة داخل المدار في هيئة الموزة .[19][20]
- الانصهار بالقصور الذاتي للبطانة الممغنطة (MagLIF) Magnetized Liner Inertial Fusion- قرصة على شكل Z من الوقود الساخن الممغنط مسبقًا داخل بطانة معدنية ، مما قد يؤدي إلى اشتعال وطاقة اندماج عملية باستخدام محرك طاقة نبضي أكبر.[21]
السلوك الشائع
قد تصبح القرصات غير مستقرة .[22] و تشع الطاقة عبر الطيف الكهرومغناطيسي بأكمله بما في ذلك موجات الراديو ، والميكروويف ، والأشعة تحت الحمراء ، والأشعة السينية ، [23] وأشعة غاما ، [24] وإشعاع السنكروترون ، [25] والضوء المرئي . كما أنها تنتج النيوترونات كناتج للاندماج.[26]

التطبيقات والأجهزة
تستخدم القرصات لتوليد الأشعة السينية وتستخدم الحقول المغناطيسية الشديدة المتولدة في التشكيل الكهرومغناطيسي للمعادن. لديهم أيضًا تطبيقات في حزم الجسيمات [27] بما في ذلك أسلحة حزمة الجسيمات ، [28] وفي دراسات الفيزياء الفلكية [29] وقد اقترح استخدامها في محركات الدفع الفضائي.[30] تم بناء عدد من آلات القرص الكبيرة لدراسة قوة الاندماج ؛ نذكر هنا عدة منها:
- MAGPIE A Z- قرصة شكلت في إمبريال كوليدج. هذا يفرغ كمية كبيرة من التيار عبر سلك. في ظل هذه الظروف ، يتحول السلك إلى بلازما ويضغط لإنتاج الاندماج.[31]
- منشأة الطاقة النبضية Z في مختبرات سانديا الوطنية.
- جهاز ZETA في كولهام ، إنجلترا
- حلقة ماديسون المتناظرة في جامعة ويسكونسن ، ماديسون
- تجربة المجال المعكوس في إيطاليا.
- تركيز البلازما الكثيف في نيو جيرسي
- جامعة نيفادا ، رينو (الولايات المتحدة الأمريكية)
- جامعة كورنيل (الولايات المتحدة الأمريكية)
- جامعة ميتشجن (الولايات المتحدة الأمريكية)
- جامعة كاليفورنيا ، سان دييغو (الولايات المتحدة الأمريكية)
- جامعة واشنطن (الولايات المتحدة الأمريكية)
- جامعة الرور (ألمانيا)
- École Polytechnique (فرنسا)
- معهد وايزمان للعلوم (إسرائيل)
- جامعة أوتونوما ميتروبوليتانا (المكسيك).
- شركة <a href="https://en.wikipedia.org/wiki/Zap_Energy" rel="mw:ExtLink" title="Zap Energy" class="cx-link" data-linkid="135">Zap Energy</a> (الولايات المتحدة الأمريكية)
سحق العلب مع تأثير قرصة

يصنع العديد من عشاق الإلكترونيات عالية الجهد أجهزة التشكيل الكهرومغناطيسية الخام الخاصة بهم.[32][33][34] يستخدمون تقنيات الطاقة النبضية لإنتاج قرصة ثيتا قادرة على سحق علبة مشروب غازي من الألومنيوم باستخدام قوى لورنتز التي تنشأ عندما يتم تحفيز تيارات شديدة في العلبة بواسطة مجال مغناطيسي قوي من الملف الأساسي.[35][36]
تتكون كسّارة علب الألمنيوم الكهرومغناطيسية من أربعة مكونات رئيسية: مصدر طاقة تيار مستمر عالي الجهد ، الذي يوفر مصدرًا للطاقة الكهربائية ، ومكثفًا كبيرًا لتفريغ الطاقة لتجميع الطاقة الكهربائية ، ومفتاح جهد عالي أو فجوة شرارة ، وملف قوي (قادر على تحمل ضغط مغناطيسي عالٍ) يمكن من خلاله تفريغ الطاقة الكهربائية المخزنة بسرعة من أجل توليد مجال مغناطيسي قوي مماثل (انظر الرسم البياني أدناه).

من الناحية العملية يعد هذا الجهاز أكثر تعقيدًا إلى حد ما مما يوحي به الرسم التخطيطي ، بما في ذلك المكونات الكهربائية التي تتحكم في التيار من أجل تعظيم الضغط الناتج ، ولضمان عمل الجهاز بأمان. لمزيد من التفاصيل ، انظر الملاحظات.[37]
التاريخ
ربما حدث أول إنشاء للقرصة Z في المختبر في عام 1790 في هولندا عندما أحدث مارتينوس فان ماروم انفجارًا عن طريق تفريغ 100 جرة ليدن Leyden jars في سلك.[39] لم تُفهم هذه الظاهرة حتى عام 1905 ، عندما قام بولوك وباراكلوف [1] بالتحقيق في طول أنبوب نحاسي مضغوط ومشوه من مانع الصواعق بعد أن ضربه البرق. أظهر تحليلهم أن القوى الناتجة عن تفاعل تدفق التيار الكبير مع المجال المغناطيسي الخاص به يمكن أن تسبب الضغط والتشويه. تم نشر تحليل نظري مشابه ومستقل على ما يبدو لتأثير القرصة في المعادن السائلة بواسطة Northrup في عام 1907.[40] التطور الرئيسي التالي نــُشر في عام 1934 لتحليل توازن الضغط الشعاعي في قرصة Z ثابتة بأجراها بينيت [41] (انظر القسم التالي للحصول على التفاصيل).
بعد ذلك ، كان التقدم التجريبي والنظري على القرصة مدفوعًا بأبحاث قوة الاندماج . في مقالهم حول "مصفوفة سلكية Z-pinch-array : مصدر أشعة سينية قوي لـ ICF ، للمؤلف. MG Haines et al كتبه عن "التاريخ المبكر للقرصات Z".[42]
- في عام 1946 ، قدم طومسون وبلاكمان براءة اختراع لمفاعل اندماجي قائم على قرص Z حلقي [43] مع مجال مغناطيسي رأسي إضافي. ولكن في عام 1954 ، نشر كروسكال وشوارزشيلد [44] نظريتهم حول عدم استقرار MHD في ضغط Z. في عام 1956 ، ألقى كورشاتوف محاضرته الشهيرة في هارويل والتي أظهرت وجود النيوترونات غير الحرارية ووجود عدم استقرار m = 0 و m = 1 في قرصة الديوتيريوم.[45] في عام 1957 ، تنبأ بيز [46] وبراجينسكي [47][48] بشكل مستقل بانهيار إشعاعي في قرص Z تحت توازن الضغط عندما يتجاوز التيار 1.4 مللي أمبير في الهيدروجين. (إن التبديد اللزج بدلاً من المقاومة للطاقة المغناطيسية التي تمت مناقشتها أعلاه وفي [49] من شأنه أن يمنع الانهيار الإشعاعي).
في عام 1958 ، تم إنجاز أول تجربة اندماج نووي حراري مضبوط في العالم باستخدام آلة ثيتا ، وهي قرصة تسمى Scylla I في مختبر لوس ألاموس الوطني . حيث تم تحويل أسطوانة مليئة بالديوتيريوم إلى بلازما وضغطها إلى 15 مليون درجة مئوية تحت تأثير قرصة ثيتا .[7] وأخيرًا في إمبريال كوليدج في عام 1960 ، بقيادة ر. لاثام ، ظهر عدم استقرار هضبة رايلي ، وتم قياس معدل نموها بضغطة Z ديناميكية.[50]
تحليل التوازن
بعد واحد
في فيزياء البلازما تتم دراسة ثلاثة أشكال هندسية للقرصة بشكل شائع: θ-pinch ، و Z-pinch ، و screw pinch. وجميعها أسطواني الشكل. الاسطوانة متماثلة في الاتجاه المحوري ( z ) واتجاهات السمتية (θ). يتم تسمية القرصات أحادية البعد طبقا لاتجاه الحركة الجارية .
القرصة θ
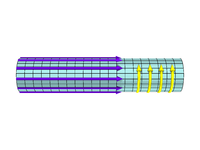
للقرصة θ مجال مغناطيسي موجه في اتجاه z وتيار مغناطيسي كبير موجه في اتجاه θ. باستخدام قانون Ampère الدائري (مع تجاهل مصطلح الإزاحة)
بما أن B ليست سوى دالة لـ r ، فيمكننا تبسيط ذلك
لذا تشير J إلى الاتجاه θ.
وعلى ذلك فإن حالة التوازن ( ) للقرصة θ تقرأ:
القرصات θ تميل إلى أن تكون مقاومة لعدم استقرار البلازما ؛ هذا يرجع جزئيًا إلى نظرية ألففين (المعروفة أيضًا باسم نظرية التدفق المتجمد).
قرصة Z

للقرصة Z مجال مغناطيسي في اتجاه θ والتيار J يتدفق في اتجاه z . مرة أخرى ، بموجب قانون أمبير للكهرباء الساكنة ،
وهكذا فإن حالة التوازن ، ، للقرصة Z تقرأ:
نظرًا لأن الجسيمات في البلازما تتبع خطوط المجال المغناطيسي بشكل أساسي ، فإن قرصات Z تقودها في دوائر. لذلك ، فهي تميل إلى امتلاك خصائص حبس ممتازة.
قرصة القلاووظ
قرصة اللولب هي محاولة للجمع بين جوانب الاستقرار للقرصة θ وجوانب الحبس للقرصة Z. ونشير مرة أخرى إلى قانون أمبير ،
لكن هذه المرة يحتوي الحقل B على المركبة θ والمركبة z
إذن في هذه المرة تحتوي J على مركبة في اتجاه z ومركبة في اتجاه.
أخيرًا نصل إلى حالة التوازن ( ) للقرصة القلاووظية (لولبية) ، وتقرأ:
قرصة المسمار عبر تصادم الدوامات البصرية
قد يتم إنتاج قرصة اللولب في بلازما الليزر عن طريق تصادم الدوامات الضوئية ذات المدة القصيرة جدًا.[51] لهذا الغرض ، يجب أن تكون الدوامات الضوئية مترافقة الطور.[52] بهذا يكون توزيع المجال المغناطيسي هنا أيضا بواسطة قانون أمبير:
ثنائي البعد
مشكلة شائعة مع القرصات أحادية البعد هي خسائر النهاية. تتم معظم حركة الجسيمات على طول المجال المغناطيسي. مع قرصة θ والقرصة اللولبية ، يؤدي ذلك إلى خروج الجسيمات من نهاية الماكينة بسرعة كبيرة ، مما يؤدي إلى فقدان الكتلة والطاقة. إلى جانب هذه المشكلة ، فإن قرص Z لديه مشاكل استقرار كبيرة. على الرغم من أن الجسيمات يمكن أن تنعكس إلى حد ما مع [المرآة المغناطيسية]] ، إلا أنها تسمح للعديد من الجسيمات بالمرور. الطريقة الشائعة للتغلب على هذه الخسائر الطرفية ، هي ثني الأسطوانة في شكل طارة. لسوء الحظ ، فإن هذا يكسر التناظر ، حيث أن المسارات على الجزء الداخلي (الجانب الداخلي) من الطارة أقصر من المسارات المماثلة على الجزء الخارجي (الجانب الخارجي). وبالتالي ، هناك حاجة إلى نظرية جديدة. أدى هذا إلى ظهور معادلة جراد-شافرانوف الشهيرة. أسفرت الحلول العددية لمعادلة جراد-شافرانوف أيضًا عن بعض التوازن ، وعلى الأخص تلك الخاصة بـ ضغط المجال المعكوس.

ثلاثة أبعاد
قالب:اعتبارًا من ، لا توجد نظرية تحليلية متماسكة للتوازن ثلاثي الأبعاد. النهج العام لإيجاد مثل هذا التوازن هو حل معادلات MHD المثالية الفراغية. أسفرت الحلول العددية عن تصميمات لـ نجمي. تستفيد بعض الآلات من تقنيات التبسيط مثل التناظر الحلزوني (على سبيل المثال ، التجربة الحلزونية المتماثلة في جامعة ويسكونسن). ومع ذلك ، بالنسبة للتكوين التعسفي ثلاثي الأبعاد ، توجد علاقة توازن ، شبيهة بعلاقة التكوينات 1-D:
حيث κ انحناء المتجه المعرف بـ :
مع "ب" متجه الوحدة المماس إلى "ب".
المعالجة الرسمية
علاقة بينيت
ضع في اعتبارك عمودًا أسطوانيًا من شبه محايد مؤين بالكامل <! - يفترض هذا الاشتقاق أن البلازما شبه محايدة ، وإلا لا يمكن التعبير عن N i و N e على أنهما واحد N. بالطبع ، يمكن للمرء أن يفترض بسهولة أن هذا كان ضمنيًا. التوضيح قد لا يكون ضروريا. -> بلازما ، ذات مجال كهربائي محوري ، تنتج كثافة تيار محوري ، "" j "" ، وما يرتبط بها من مجال مغناطيسي سمتي ، "" ب "". عندما يتدفق التيار عبر المجال المغناطيسي الخاص به ، يتم إنشاء قرصة بكثافة قوة شعاعية داخلية تبلغ "" j x B "". في حالة مستقرة مع توازن القوى:
حيث ∇p هو تدرج الضغط المغناطيسي ، و p e و p i هما ضغط الإلكترون والأيون ، على التوالي. ثم استخدم معادلة ماكسويل
وطبقا لقانون الغاز المثالي:
,
ونحصل على
- (علاقة بينيت)
حيث "N" هو عدد الإلكترونات لكل وحدة طول على طول المحور ، و "T e " و "T i " هي الإلكترون والأيون درجات الحرارة ، "I" هو تيار الحزمة الكلي ، و "k" هو ثابت بولتزمان.
علاقة بينيت العامة
علاقة بينيت المعممة تعتبر قرصة بلازما أسطوانية تحمل تيارًا محاذاة للمجال المغناطيسي تخضع للدوران عند التردد الزاوي ω تعتبر "علاقة بينيت المعممة" قرصة بلازما أسطوانية تحمل تيارًا مغناطيسيًا محاذاة للمجال المغناطيسي تخضع للدوران عند التردد الزاوي ω. على طول محور أسطوانة البلازما تتدفق كثافة التيار j z ، مما ينتج عنه حقل مغناطيسي سمتي Β φ . مشتق أصلاً من Witalis ، [56] تؤدي علاقة بينيت المعممة إلى:[57]
- حيث يكون للبلازما الأسطوانية الحاملة للتيار والمحاذاة للمجال المغناطيسي نصف قطر `` a ،
- J 0 هي اللحظة الكلية للقصور الذاتي فيما يتعلق بالمحور z ،
- "W" ⊥kin هي الطاقة الحركية لكل وحدة طول بسبب حركة الحزمة المستعرضة إلى محور الحزمة
- W B z هي طاقة B z المتسقة ذاتيًا لكل وحدة طول
- W E z هي طاقة E z المتسقة ذاتيًا لكل وحدة طول
- "W" k هي طاقة حرارية لكل وحدة طول
- I ( a ) هو التيار المحوري داخل نصف القطر a ( r في الرسم التخطيطي)
- N ( a ) هو العدد الإجمالي للجسيمات لكل وحدة طول
- "E" r هو المجال الكهربائي الشعاعي
- "E" φ هو المجال الكهربائي الدوراني
المصطلحات الموجبة في المعادلة هي قوى تمدد بينما تمثل المصطلحات السالبة قوى ضغط الحزمة.
علاقة Carlqvist
علاقة Carlqvist ، التي نشرتها Per Carlqvist في عام 1988 ، [12] هي تخصص لعلاقة بينيت المعممة (أعلاه) ، في حالة أن الضغط الحركي أصغر بكثير عند حدود القرصة مقارنة بالأجزاء الداخلية. يأخذ الشكل
وينطبق على العديد من البلازما الفضائية.
يمكن توضيح علاقة Carlqvist (انظر إلى اليمين) ، وإظهار إجمالي التيار ("I") مقابل عدد الجسيمات لكل وحدة طول ("N") في قرصة بينيت. يوضح الرسم البياني أربع مناطق متميزة ماديًا. درجة حرارة البلازما باردة جدًا ( T i = T e = T n = 20 K) ، تحتوي بشكل أساسي على الهيدروجين بمتوسط كتلة جسيمية 3 × 10 −27 kg. الطاقة الحرارية W k >> πa 2 p k </ الفرعية> (أ). تظهر المنحنيات ، ΔW Bz كميات مختلفة من الطاقة المغناطيسية الزائدة لكل وحدة طول بسبب المجال المغناطيسي المحوري B z . يُفترض أن البلازما غير دورانية ، والضغط الحركي عند الحواف أصغر بكثير من الداخل.
'مناطق الرسم البياني:' (أ) في المنطقة العلوية اليسرى ، تهيمن قوة القرص. (ب) باتجاه الأسفل ، تتوازن الضغوط الحركية الخارجية مع الضغط المغناطيسي الداخلي ، ويكون الضغط الكلي ثابتًا. (ج) على يمين الخط العمودي ΔW Bz & nbsp ؛ = & nbsp ؛ 0 ، الضغط المغناطيسي يوازن ضغط الجاذبية ، وقوة القرص لا تذكر . (د) إلى يسار منحنى المنحدر ΔW Bz & nbsp ؛ = & nbsp ؛ 0 ، قوة الجاذبية لا تذكر. لاحظ أن الرسم البياني يوضح حالة خاصة لعلاقة Carlqvist ، وإذا تم استبدالها بعلاقة Bennett الأكثر عمومية ، فإن المناطق المحددة في المخطط غير صالحة.
المراجع في الثقافة
تم استخدام جهاز توليد الضغط في "Ocean's Eleven" ، حيث تم استخدامه لتعطيل شبكة الطاقة في لاس فيغاس لفترة كافية لتبدأ الشخصيات سرقتها.[58]
انظر أيضًا
- تشكيل كهرومغناطيسي
- مولد ضغط التدفق يضخ بمتفجر
- طاقة الاندماج
- تشكيل المجال المعكوس
- List of plasma physics articles
- حلقة ماديسون المتماثلة (reversed field pinch)
- توكاماك DIII-D
- حلقة ماديسون المتماثلة
المراجع
- ^ أ ب Pollock J A and Barraclough S (1905) Proc. R. Soc. New South Wales 39 131
- ^ Buneman، O. (1961). "The Bennett Pinch". في Drummond، James E. (المحرر). Plasma Physics. New York: McGraw-Hill. ص. 202. Bibcode:1961plph.conf..202B. مؤرشف من الأصل في 2022-10-24. LOC 60-12766.
- ^ Lee، S. (1983). "Energy balance and the radius of electromagnetically pinched plasma columns". Plasma Physics. ج. 25 ع. 5: 571–576. Bibcode:1983PlPh...25..571L. DOI:10.1088/0032-1028/25/5/009.
- ^ Schmidt، Helmut (1966). "Formation of a Magnetic Pinch in InSb and the Possibility of Population Inversion in the Pinch". Physical Review. ج. 149 ع. 2: 564–573. Bibcode:1966PhRv..149..564S. DOI:10.1103/physrev.149.564.
- ^ Severnyi، A. B. (1959). "On the Appearance of Cosmics Rays in the Pinch Effect in Solar Flares". Soviet Astronomy. ج. 3: 887. Bibcode:1959SvA.....3..887S.
- ^ Zueva، N. M.؛ Solov'ev، L. S.؛ Morozov، A. I. (1976). "Nonlinear instability of plasma pinches". Journal of Experimental and Theoretical Physics Letters. ج. 23: 256. Bibcode:1976JETPL..23..256Z.
- ^ أ ب Phillips، James (Winter 1983). "Magnetic Fusion". Los Alamos Science. ص. 64–67.
- ^ Rai، J.؛ Singh، A. K.؛ Saha، S. K (1973). "Magnetic field within the return stroke channel of lightning". Indian Journal of Radio and Space Physics. ج. 2: 240–242. Bibcode:1973IJRSP...2..240R.
- ^ Galperin، Iu. I.؛ Zelenyi، L. M.؛ Kuznetsova، M. M. (1986). "Pinching of field-aligned currents as a possible mechanism for the formation of raylike auroral forms". Kosmicheskie Issledovaniia. ج. 24: 865–874. Bibcode:1986KosIs..24..865G.
- ^ Syrovatskii، S. I. (1981). "Pinch sheets and reconnection in astrophysics". Annual Review of Astronomy and Astrophysics. ج. 19: 163–229. Bibcode:1981ARA&A..19..163S. DOI:10.1146/annurev.aa.19.090181.001115.
- ^ Airapetyan، V. S.؛ Vikhrev، V. V.؛ Ivanov، V. V.؛ Rozanova، G. A. (1990). "Pinch Mechanism of Energy Release of Stellar Flares". Astrophysics. ج. 32 ع. 3: 230–235. Bibcode:1990Ap.....32..230A. DOI:10.1007/bf01005504.
- ^ أ ب Carlqvist، Per (مايو 1988). "Cosmic electric currents and the generalized Bennett relation". Astrophysics and Space Science. ج. 144 ع. 1–2: 73–84. Bibcode:1988Ap&SS.144...73C. DOI:10.1007/BF00793173. مؤرشف من الأصل في 2022-12-31.
- ^ Biskamp، Dieter (1997). Nonlinear Magnetohydrodynamics. كامبريدج, England: Cambridge University Press. ص. 130. ISBN:0-521-59918-0.
- ^ Basu، Dipak K. (8 أكتوبر 2018). Dictionary of Material Science and High Energy Physics. ص. 315. ISBN:978-0-8493-2889-3. مؤرشف من الأصل في 2022-12-31.
- ^ Srivastava، K. M.؛ Vyas، D. N. (أغسطس 1982). "Non-linear analysis of the stability of the screw pinch". Astrophysics and Space Science. ج. 86 ع. 1: 71–89. Bibcode:1982Ap&SS..86...71S. DOI:10.1007/BF00651831. مؤرشف من الأصل في 2022-10-24.
- ^ See "MHD Equilibria" in Introduction to Plasma Physics by I.H.Hutchinson (2001) نسخة محفوظة 2022-10-13 على موقع واي باك مشين.
- ^ Srivastava، K. M.؛ Waelbroeck، F. (1976). "On the stability of the screw pinch in the CGL model". Journal of Plasma Physics. ج. 16 ع. 3: 261. Bibcode:1976JPlPh..16..261S. DOI:10.1017/s0022377800020201.
- ^ Anderson، O. A.؛ Furth، H. P.؛ Stone، J. M.؛ Wright، R. E. (نوفمبر 1958). "Inverse Pinch Effect". Physics of Fluids. ج. 1 ع. 6: 489–494. Bibcode:1958PhFl....1..489A. DOI:10.1063/1.1724372.
- ^ Helander، P.؛ Akers، R. J.؛ Valovič، M. (3 نوفمبر 2005). "The effect of non-inductive current drive on tokamak transport". Plasma Physics and Controlled Fusion. ج. 47 ع. 12B: B151–B163. Bibcode:2005PPCF...47B.151H. DOI:10.1088/0741-3335/47/12b/s12.
- ^ "Plasma Physics: Third Edition" Page 266 https://books.google.co.uk/books?id=4cHkd77TSHcC&pg=PA266&dq=Ware+pinch&hl=en&sa=X&ei=aZsVVdvZF5L8gwSO_oDoDw&ved=0CCYQ6AEwAQ#v=onepage&q=Ware%20pinch&f=false نسخة محفوظة 2018-11-16 على موقع واي باك مشين.
- ^ Slutz، Stephen؛ Vesey، Roger A. (2012). "High-Gain Magnetized Inertial Fusion". Physical Review Letters. ج. 108 ع. 2: 025003. Bibcode:2012PhRvL.108b5003S. DOI:10.1103/PhysRevLett.108.025003. PMID:22324693.
- ^ Hardee، P. E. (1982). "Helical and pinching instability of supersonic expanding jets in extragalactic radio sources". Astrophysical Journal. ج. 257: 509–526. Bibcode:1982ApJ...257..509H. DOI:10.1086/160008.
- ^ Pereira، N. R.؛ وآخرون (1988). "X-rays from Z-pinches on relativistic electron-beam generators". Journal of Applied Physics. ج. 64 ع. 3: R1–R27. Bibcode:1988JAP....64....1P. DOI:10.1063/1.341808.
- ^ Wu، Mei؛ Chen، Li؛ Li، Ti-Pei (2005). "Polarization in Gamma-Ray Bursts Produced by Pinch Discharge". Chinese Journal of Astronomy & Astrophysics. ج. 5 ع. 1: 57–64. arXiv:astro-ph/0501334. Bibcode:2005ChJAA...5...57W. DOI:10.1088/1009-9271/5/1/007.
- ^ Peratt, A.L., "Synchrotron radiation from pinched particle beams", (1998) Plasma Physics: VII Lawpp 97: Proceedings of the 1997 Latin American Workshop on Plasma Physics, Edited by Pablo Martin, Julio Puerta, Pablo Martmn, with reference to Meierovich, B. E., "Electromagnetic collapse. Problems of stability, emission of radiation and evolution of a dense pinch" (1984) Physics Reports, Volume 104, Issue 5, p. 259-346. نسخة محفوظة 2016-12-23 على موقع واي باك مشين.
- ^ Anderson، Oscar A.؛ وآخرون (1958). "Neutron Production in Linear Deuterium Pinches". Physical Review. ج. 110 ع. 6: 1375–1387. Bibcode:1958PhRv..110.1375A. DOI:10.1103/physrev.110.1375. مؤرشف من الأصل في 2022-12-31.
- ^ Ryutov، D. D.؛ Derzon، M. S.؛ Matzen، M. K (2000). "The physics of fast Z pinches". Reviews of Modern Physics. ج. 72 ع. 1: 167–223. Bibcode:2000RvMP...72..167R. DOI:10.1103/revmodphys.72.167. مؤرشف من الأصل في 2022-12-31.
- ^ Andre Gsponer, "Physics of high-intensity high-energy particle beam propagation in open air and outer-space plasmas" (2004) https://arxiv.org/abs/physics/0409157 نسخة محفوظة 2022-04-29 على موقع واي باك مشين.
- ^ Peratt, Anthony L., "The role of particle beams and electrical currents in the plasma universe" (1988) Laser and Particle Beams (ISSN 0263-0346), vol. 6, Aug. 1988, p. 471-491. نسخة محفوظة 2010-01-13 على موقع واي باك مشين.
- ^ "Z-Pinch Pulsed Plasma Propulsion Technology Development"Final Report Advanced Concepts Office (ED04) Marshall Space Flight Center October 8, 2010, Tara Polsgrove, Et Al.
- ^ http://dorland.pp.ph.ic.ac.uk/magpie/?page_id=239 نسخة محفوظة 2014-11-05 على موقع واي باك مشين. "Wire Arrays Z-Pinch" accessed: 3-27-2015
- ^ LaPointe، Robert. "High Voltage Devices and Experiments". مؤرشف من الأصل في 2023-04-03. اطلع عليه بتاريخ 2013-02-21.
- ^ Tristan. "Electromagnetic Can Crusher". مؤرشف من الأصل في 2023-01-29. اطلع عليه بتاريخ 2013-02-21.
- ^ Borros، Sam. "Solid State Can Crusher". مؤرشف من الأصل في 2023-02-26. اطلع عليه بتاريخ 2013-02-21.
- ^ "MagnetoPulS". Magnet-Physik, Dr. Steingroever GmbH. 2002. مؤرشف من الأصل في 2003-05-22. اطلع عليه بتاريخ 2013-02-21.
- ^ "Industrial Application of the Electromagnetic Pulse Technology" (PDF). white paper. PSTproducts GmbH. يونيو 2009. مؤرشف من الأصل (PDF) في 2011-07-15. اطلع عليه بتاريخ 2013-02-21.
- ^ Examples of electromagnetic pinch can crushers can be found at (a) Bob LaPointe's site on High Voltage Devices and Experiments (b) Tristran's Electromagnetic Can Crusher (including schematic) (c) Sam Borros's Solid State Can Crusher نسخة محفوظة 2021-10-25 على موقع واي باك مشين.
- ^ See also the IEEE History Center, "Evolution of the IEEE Logo" March 1963; see also the comments in "Laboratory Astrophysics" نسخة محفوظة 2005-11-23 على موقع واي باك مشين.
- ^ van Marum M 1790 Proc. 4th Int. Conf. on Dense Z-Pinches (Vancouver 1997) (Am. Inst. Phys. Woodbury, New York, 1997) Frontispiece and p ii
- ^ Northrup، Edwin F. (1907). "Some Newly Observed Manifestations of Forces in the Interior of an Electric Conductor". American Physical Society (APS). Series I. ج. 24 ع. 6: 474–497. Bibcode:1907PhRvI..24..474N. DOI:10.1103/physrevseriesi.24.474. ISSN:1536-6065. مؤرشف من الأصل في 2022-12-31.
- ^ Bennett، Willard H. (1934). "Magnetically Self-Focussing Streams". Phys. Rev. ج. 45 ع. 12: 890–897. Bibcode:1934PhRv...45..890B. DOI:10.1103/physrev.45.890.
- ^ Haines، M G؛ Sanford، T W L؛ Smirnov، V P (2005). "Wire-array Z-pinch: a powerful x-ray source for ICF". Plasma Phys. Control. Fusion. ج. 47 ع. 12B: B1–B11. Bibcode:2005PPCF...47B...1H. DOI:10.1088/0741-3335/47/12b/s01.
- ^ Thompson، G. P.؛ Blackman؛ Haines، M. G. (1996). "Historical Perspective: Fifty years of controlled fusion research". Plasma Physics and Controlled Fusion. ج. 38 ع. 5: 643–656. Bibcode:1996PPCF...38..643H. DOI:10.1088/0741-3335/38/5/001.
- ^ Kruskal، M D؛ Schwarzschild (1954). "Some Instabilities of a Completely Ionized Plasma". Proc. R. Soc. Lond. A. ج. 223 ع. 1154: 348–360. Bibcode:1954RSPSA.223..348K. DOI:10.1098/rspa.1954.0120.
- ^ Kurchatov I V (1957) J. Nucl. Energy 4 193
- ^ Pease، R S (1957). "Equilibrium Characteristics of a Pinched Gas Discharge Cooled by Bremsstrahlung Radiation". Proc. Phys. Soc. Lond. ج. 70 ع. 1: 11–23. Bibcode:1957PPSB...70...11P. DOI:10.1088/0370-1301/70/1/304.
- ^ Braginskii S I 1957 Zh. Eksp. Teor. Fiz 33 645
- ^ Braginskii S I 1958 Sov. Phys.—JETP 6 494
- ^ Haines M G et al. 2005 Phys. Rev. Lett.. submitted; see also EPS Conf. on Plasma Physics 2004 (London, UK) paper 73
- ^ Curzon، F. L.؛ وآخرون (1960). "Experiments on the Growth Rate of Surface Instabilities in a Linear Pinched Discharge". Proc. R. Soc. Lond. A. ج. 257 ع. 1290: 386–401. Bibcode:1960RSPSA.257..386C. DOI:10.1098/rspa.1960.0158.
- ^ A.Yu.Okulov. "Laser singular Theta-pinch", Phys.Lett.A, v.374, 4523-4527, (2010) نسخة محفوظة 2022-10-25 على موقع واي باك مشين.
- ^ Optical phase conjugation and electromagnetic momenta
- ^ الديناميكا المائية المثالية: وجهات نظر حديثة في الطاقة. جيفري ب. فريدبرج. معهد ماساتشوستس للتكنولوجيا. كامبريدج ، ماساتشوستس. المطبعة الكاملة - نيويورك ولندن - 1987. (ص 86 ، 95)
- ^ Trubnikov، Boris A (1992). "فرضية جديدة لتوليد الأشعة الكونية في قرصات البلازما". IEEE Transactions on Plasma Science (ط. 6): 898–904. DOI:10.1109 / 27.199547.
{{استشهاد بدورية محكمة}}: الوسيط غير المعروف|البيب كود=تم تجاهله (مساعدة)، الوسيط غير المعروف|الحجم=تم تجاهله (مساعدة)، وتأكد من صحة قيمة|doi=(مساعدة) - ^ "تكوين PLASMAK و Ball Lightning" (PDF نسخة محفوظة 13 يوليو 2012 على موقع واي باك مشين.) تم تقديمها في الندوة الدولية حول Ball Lightning ؛ يوليو 1988
- ^ Witalis، E.A. المراجعة الفيزيائية أ - الفيزياء العامة ، السلسلة الثالثة ، المجلد. 24 نوفمبر 1981 ، ص. 2758–2764
- ^ أنتوني إل. بيرات ، "فيزياء الكون البلازما" ، 1992 Springer-Verlag ، (ردمك 0-387-97575-6)
- ^ [https: //www.aps. org / منشورات / apsnews / 200203 / oceans-eleven.cfm "The Con-Artist Physics of 'Ocean's Eleven'"]. American Physical Society. مارس 2002.
{{استشهاد بخبر}}: تحقق من قيمة|مسار=(مساعدة)
مصادر خارجية
- Examples of electromagnetically shrunken coins and crushed cans
- Theory of electromagnetic coin shrinking
- The Known History of "Quarter Shrinking"
- Can crushing info using electromagnetism among other things
- The MAGPIE project at Imperial College London is used to study wire array Z-pinch implosions.


