عجلي فوقي

عجلي فوقي فيه R = 3 ،r = 1 ،d = 1/2

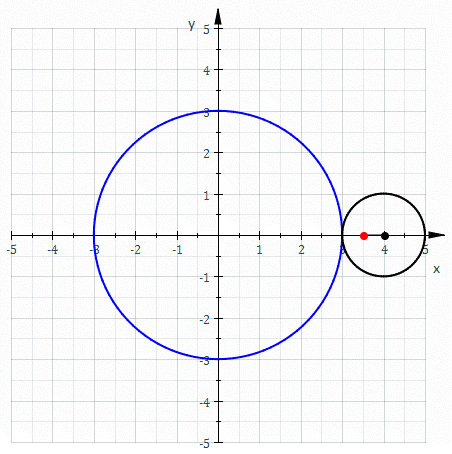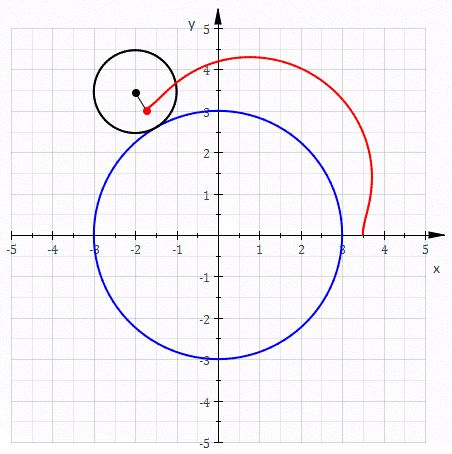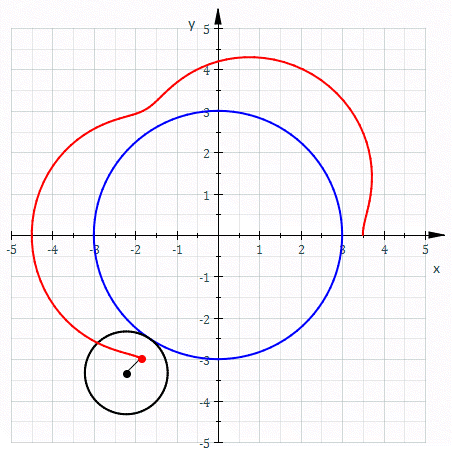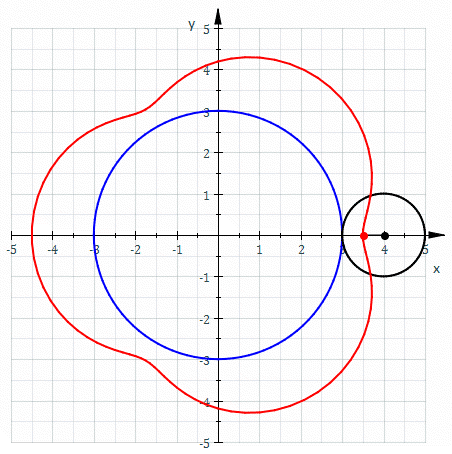
العجلي الفوقي أو الدحروج العام الفوقي (بالإنجليزية: Epitrochoid)‏ هي دحروجة تولدها نقطة واقعة على المستقيم المار بمركز دائرة نصف قطرها r تتدحرج دون انزلاق على المحيط الخارجي لدائرة أخرى ثابتة نصف قطرها R، بحيث تكون d هي المسافة بين النقطة ومركز الدائرة الخارجية. يعتبر العجلي الفوقي تعميمًا للدويري الفوقي.

المعادلتان الوسيطيتان للعجلي الفوقي هما:

$x(\theta )=(R+r)\cos \theta -d\cos \left(\frac{R+r}{r}\theta \right),$

$y(\theta )=(R+r)\sin \theta -d\sin \left(\frac{R+r}{r}\theta \right).$

المعادلة القطبية للعجلي الفوقي هي:

$r(\theta {)}^2=(R+r{)}^2-2d(R+r)\cos \left(\frac{R}{r}\theta \right)+d^2,$

يوجد حالتان خاصتان للعجلي الفوقي هما:

1. عندما R = r نحصل على منحنى ليماسون
2. عندما d = r نحصل على دويري فوقي

مدارات الكواكب في نظام مركزية الأرض التي أقامها الفلكي السكندري «بطليموس» هي منحنيات عجلية فوقية

غرفة الاحتراق في محرك فانكل هي منحنى عجلي فوقي

انظر أيضًا

• دويري
• دويري فوقي
• دويري تحتي
• عجلي
• عجلي تحتي

المراجع

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. ص. 160–164.

وصلات خارجية

• Flash Animation of Epitrochoid
• Epitrochoid at Mathworld
• Visual Dictionary of Special Plane Curves on Xah Lee 李杀网
• Interactive simulation of the geocentric graphical representation of planet paths