|
تضامنًا مع حق الشعب الفلسطيني |
دوال ثيتا لنيفيل
اذهب إلى التنقل
اذهب إلى البحث
في الرياضيات، دوال ثيتا لنيفيل (بالإنجليزية: Neville theta functions) التي سميت باسم ،[1] معرفة على النحو التالي:[2][3][4]
هو التكامل الإهليلجي التام من النوع الأول، و هو النُوم [English] الإهليلجي.
العلاقة بدوال أخرى
يمكن التعبير عن دوال ثيتا لنيفيل بدلالة دوال ثيتا لجاكوبي [5]
حيث .
ترتبط دوال ثيتا لنيفيل بدوال جاكوبي الإهليلجية [English]. إذا كانت هي دالة جاكوبي الإهليلجية، فإن:
أمثلة
نعوض z = 2.5, m = 0.3 في التعريفات المذكورة أعلاه لدوال ثيتا لنيفيل (باستخدام برنامج ميبل) بمجرد الحصول على ما يلي (بما يتفق مع نتائج ماثورلد ولفرام).[6]
تناظر
تمثيلات بيانية عقدية ثلاثية الأبعاد

|
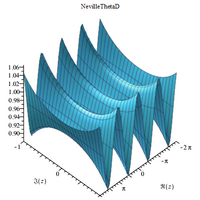
|

|
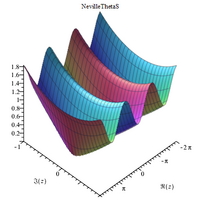
|
مراجع
- ^ * Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. <nowiki>ISBN 978-0-486-61272-0</nowiki>. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- ^ Neville، E. H. (Eric Harold) (1944). Jacobian Elliptic Functions. Oxford Clarendon Press. مؤرشف من الأصل في 2008-06-17.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ wolfram Mathematic نسخة محفوظة 2016-10-21 على موقع واي باك مشين.
- ^ wolfram math نسخة محفوظة 2020-06-14 على موقع واي باك مشين.
- ^ Olver، المحرر (22 ديسمبر 2017). "NIST Digital Library of Mathematical Functions (Release 1.0.17)". National Institute of Standards and Technology. مؤرشف من الأصل في 2020-04-06. اطلع عليه بتاريخ 2018-02-26.
- ^ "NevilleThetaC(2.5,0.3) - Wolfram|Alpha". www.wolframalpha.com. مؤرشف من الأصل في 2020-06-14. اطلع عليه بتاريخ 2020-06-14.