|
تضامنًا مع حق الشعب الفلسطيني |
العلاقة بين الرياضيات والفيزياء

كانت العلاقة بين الرياضيات والفيزياء موضوعًا لدراسة الفلاسفة والرياضيين والفيزيائيين منذ العصور القديمة، ومؤخراً أيضًا من قبل المؤرخين والمعلمين.[2] تعتبر بشكل عام علاقة حميمية كبيرة،[3] وقد تم وصف الرياضيات بأنها «أداة أساسية للفيزياء»[4] ووصفت الفيزياء بأنها «مصدر غني للإلهام والبصيرة في الرياضيات».[5]
في عمله السماع الطبيعي، أحد الموضوعات التي عالجها أرسطو تدور حول كيفية اختلاف الدراسة التي أجراها علماء الرياضيات عن تلك التي قام بها علماء الفيزياء.[6] يمكن العثور على الاعتبارات المتعلقة بكون الرياضيات لغة الطبيعة في أفكار الفيثاغورية: المعتقدات القائلة بأن «الأرقام تحكم العالم» و«كل شيء رقم»،[7][8] وبعد ألفي عام عبر غاليليو غاليلي أيضًا: «كتاب الطبيعة مكتوب بلغة الرياضيات».[9][10]
قبل تقديم دليل رياضي لصيغة حجم الكرة، استخدم أرخميدس التفكير المادي لاكتشاف الحل (تخيل موازنة الأجسام على مقياس).[11] منذ القرن السابع عشر، ظهرت العديد من أهم التطورات في الرياضيات بدافع من دراسة الفيزياء، واستمر هذا في القرون التالية (على الرغم من أن الرياضيات في القرن التاسع عشر بدأت تصبح مستقلة بشكل متزايد عن الفيزياء).[12][13] كان إنشاء حساب التفاضل والتكامل وتطويره مرتبطًا بقوة باحتياجات الفيزياء.[14] كانت هناك حاجة إلى لغة رياضية جديدة للتعامل مع الديناميكيات الجديدة التي نشأت من عمل العلماء مثل غاليليو غاليلي وإسحاق نيوتن.[15] خلال هذه الفترة كان هناك القليل من التمييز بين الفيزياء والرياضيات؛[16] كمثال، اعتبر نيوتن الهندسة كفرع من الميكانيكا.[17] مع تقدم الوقت، بدأ استخدام الرياضيات المعقدة بشكل متزايد في الفيزياء. الوضع الحالي هو أن المعرفة الرياضية المستخدمة في الفيزياء أصبحت معقدة بشكل متزايد، كما هو الحال في نظرية الأوتار الفائقة.[18]
المسائل الفلسفية
فيما يلي بعض المسائل التي تم تناولها في فلسفة الرياضيات:
- شرح فاعلية الرياضيات في دراسة العالم المادي: «في هذه المرحلة، يظهر اللغز الذي أثار في جميع الأعمار العقول المستفسرة. كيف يمكن أن تكون الرياضيات، بعد كل شيء، نتاج الفكر البشري المستقل عن التجربة، هل هذا مناسب بشكل مثير للإعجاب لموضوعات الواقع؟» - ألبرت أينشتاين، في الهندسة والتجربة (1921).[19]
- تحديد مجال الرياضيات والفيزياء بوضوح: بالنسبة لبعض النتائج أو الاكتشافات، من الصعب تحديد المجال الذي ينتمون إليه: الرياضيات أو الفيزياء.[20]
- ما هي هندسة الفضاء المادي؟[21]
- ما هو أصل بديهيات الرياضيات؟[22]
- كيف تؤثر الرياضيات الموجودة بالفعل في إنشاء وتطوير النظريات الفيزيائية؟[23]
- هل الحساب تحليلي أم تركيبي؟ (من كانت، انظر التمييز التحليلي - التركيبي)[24]
- ما هو الاختلاف الجوهري بين إجراء تجربة فيزيائية لرؤية النتيجة وإجراء عملية حسابية لمعرفة النتيجة؟ (من مناظرة تورنغ - فيتغنشتاين)[25]
- هل تشير مبرهنات عدم الاكتمال لغودل إلى أن النظريات الفيزيائية ستكون دائمًا غير مكتملة؟ (من ستيفن هوكينج)[26][27]
- هل الرياضيات مخترعة أم مكتشفة؟ (سؤال عمره آلاف السنين، أثاره ماريو ليفيو من بين أمور أخرى)[28]
التعليم
في الآونة الأخيرة، تم تدريس هذين التخصصين بشكل منفصل، على الرغم من جميع العلاقات المتبادلة بين الفيزياء والرياضيات.[29] أدى ذلك إلى قيام بعض علماء الرياضيات المحترفين الذين كانوا مهتمين أيضًا بتعليم الرياضيات، مثل فيليكس كلاين وريتشارد كورنت وفلاديمير أرنولد وموريس كلاين، بالدعوة بقوة لتدريس الرياضيات بطريقة ترتبط ارتباطًا وثيقًا بالعلوم الفيزيائية.[30][31]
انظر أيضًا
- رياضيات بحتة
- رياضيات تطبيقية
- فيزياء نظرية
- فيزياء رياضية
- هندسة لاإقليدية
- متسلسلة فورييه
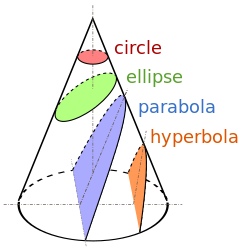
- قطع مخروطي
- قوانين كيبلر للحركة الكوكبية
- بوزيترون
- الفعالية غير المعقولة للرياضيات في العلوم الطبيعية
- الكون الرياضي
- مفارقات زينون
- نموذج رياضي
- تجريبية (فلسفة)
- منطقانية
- شكلية (فلسفة الرياضيات)
- رياضيات النسبية العامة
- نيكولا بورباكي
- رياضيات تجريبية
- تاريخ علم الفلك
المراجع
- ^ Jed Z. Buchwald؛ Robert Fox (10 أكتوبر 2013). The Oxford Handbook of the History of Physics. OUP Oxford. ص. 128. ISBN:978-0-19-151019-9. مؤرشف من الأصل في 2020-10-05.
- ^ Uhden، Olaf؛ Karam، Ricardo؛ Pietrocola، Maurício؛ Pospiech، Gesche (20 أكتوبر 2011). "Modelling Mathematical Reasoning in Physics Education". Science & Education. ج. 21 ع. 4: 485–506. Bibcode:2012Sc&Ed..21..485U. DOI:10.1007/s11191-011-9396-6. S2CID:122869677.
- ^ Francis Bailly؛ Giuseppe Longo (2011). Mathematics and the Natural Sciences: The Physical Singularity of Life. World Scientific. ص. 149. ISBN:978-1-84816-693-6. مؤرشف من الأصل في 2020-10-05.
- ^ Sanjay Moreshwar Wagh؛ Dilip Abasaheb Deshpande (27 سبتمبر 2012). Essentials of Physics. PHI Learning Pvt. Ltd. ص. 3. ISBN:978-81-203-4642-0. مؤرشف من الأصل في 2020-10-05.
- ^ Atiyah، Michael (1990). "On the Work of Edward Witten" (PDF). International Congress of Mathematicians. Japan. ص. 31–35. مؤرشف من الأصل (PDF) في 2017-03-01.
- ^ Lear، Jonathan (1990). Aristotle: the desire to understand (ط. Repr.). Cambridge [u.a.]: Cambridge Univ. Press. ص. 232. ISBN:9780521347624. مؤرشف من الأصل في 2020-10-05.
- ^ Gerard Assayag؛ Hans G. Feichtinger؛ José-Francisco Rodrigues (10 يوليو 2002). Mathematics and Music: A Diderot Mathematical Forum. Springer. ص. 216. ISBN:978-3-540-43727-7. مؤرشف من الأصل في 2020-10-05.
- ^ Al-Rasasi، Ibrahim (21 يونيو 2004). "All is number" (PDF). King Fahd University of Petroleum and Minerals. مؤرشف من الأصل في 2020-10-05. اطلع عليه بتاريخ 2015-06-13.
- ^ Aharon Kantorovich (1 يوليو 1993). Scientific Discovery: Logic and Tinkering. SUNY Press. ص. 59. ISBN:978-0-7914-1478-1. مؤرشف من الأصل في 2020-10-05.
- ^ Kyle Forinash, William Rumsey, Chris Lang, Galileo's Mathematical Language of Nature. نسخة محفوظة 27 سبتمبر 2013 على موقع واي باك مشين.
- ^ Arthur Mazer (26 سبتمبر 2011). The Ellipse: A Historical and Mathematical Journey. John Wiley & Sons. ص. 5. Bibcode:2010ehmj.book.....M. ISBN:978-1-118-21143-4. مؤرشف من الأصل في 2020-10-05.
- ^ E. J. Post, A History of Physics as an Exercise in Philosophy, p. 76. نسخة محفوظة 5 أكتوبر 2020 على موقع واي باك مشين.
- ^ Arkady Plotnitsky, Niels Bohr and Complementarity: An Introduction, p. 177. نسخة محفوظة 2020-10-05 على موقع واي باك مشين.
- ^ Roger G. Newton (1997). The Truth of Science: Physical Theories and Reality. Harvard University Press. ص. 125–126. ISBN:978-0-674-91092-8. مؤرشف من الأصل في 2020-10-05.
- ^ Eoin P. O'Neill (editor), What Did You Do Today, Professor?: Fifteen Illuminating Responses from Trinity College Dublin, p. 62. نسخة محفوظة 2020-10-05 على موقع واي باك مشين.
- ^ Timothy Gowers؛ June Barrow-Green؛ Imre Leader (18 يوليو 2010). [[رفيق برينستون للرياضيات|The Princeton Companion to Mathematics]]. Princeton University Press. ص. 7. ISBN:978-1-4008-3039-8. مؤرشف من الأصل في 2020-10-05.
{{استشهاد بكتاب}}: تعارض مسار مع وصلة (مساعدة) - ^ David E. Rowe (2008). "Euclidean Geometry and Physical Space". The Mathematical Intelligencer. ج. 28 ع. 2: 51–59. DOI:10.1007/BF02987157. S2CID:56161170.
- ^ "String theories". Particle Central. Four Peaks Technologies. مؤرشف من الأصل في 2020-10-05. اطلع عليه بتاريخ 2015-06-13.
- ^ ألبرت أينشتاين, Geometry and Experience. نسخة محفوظة 22 أكتوبر 2019 على موقع واي باك مشين.
- ^ Pierre Bergé, Des rythmes au chaos. نسخة محفوظة 8 مارس 2021 على موقع واي باك مشين.
- ^ Gary Carl Hatfield (1990). The Natural and the Normative: Theories of Spatial Perception from Kant to Helmholtz. MIT Press. ص. 223. ISBN:978-0-262-08086-6. مؤرشف من الأصل في 2021-03-09.
- ^ Gila Hanna؛ Hans Niels Jahnke؛ Helmut Pulte (4 ديسمبر 2009). Explanation and Proof in Mathematics: Philosophical and Educational Perspectives. Springer Science & Business Media. ص. 29–30. ISBN:978-1-4419-0576-5. مؤرشف من الأصل في 2021-03-08.
- ^ "FQXi Community Trick or Truth: the Mysterious Connection Between Physics and Mathematics". مؤرشف من الأصل في 2021-12-14. اطلع عليه بتاريخ 2015-04-16.
- ^ James Van Cleve Professor of Philosophy Brown University (16 يوليو 1999). Problems from Kant. Oxford University Press, USA. ص. 22. ISBN:978-0-19-534701-2. مؤرشف من الأصل في 2016-08-22.
- ^ Ludwig Wittgenstein؛ R. G. Bosanquet؛ Cora Diamond (15 أكتوبر 1989). Wittgenstein's Lectures on the Foundations of Mathematics, Cambridge, 1939. University of Chicago Press. ص. 96. ISBN:978-0-226-90426-9. مؤرشف من الأصل في 2021-03-08.
- ^ Pudlák، Pavel (2013). Logical Foundations of Mathematics and Computational Complexity: A Gentle Introduction. Springer Science & Business Media. ص. 659. ISBN:978-3-319-00119-7. مؤرشف من الأصل في 2016-05-02.
- ^ Stephen Hawking. "Godel and the End of the Universe" نسخة محفوظة 2020-05-29 على موقع واي باك مشين.
- ^ Mario Livio (أغسطس 2011). "Why math works?". Scientific American: 80–83. مؤرشف من الأصل في 2020-11-12.
- ^ Karam; Pospiech; & Pietrocola (2010). "Mathematics in physics lessons: developing structural skills" نسخة محفوظة 2021-03-01 على موقع واي باك مشين.
- ^ Stakhov "Dirac’s Principle of Mathematical Beauty, Mathematics of Harmony" نسخة محفوظة 2021-04-17 على موقع واي باك مشين.
- ^ Richard Lesh؛ Peter L. Galbraith؛ Christopher R. Haines؛ Andrew Hurford (2009). Modeling Students' Mathematical Modeling Competencies: ICTMA 13. Springer. ص. 14. ISBN:978-1-4419-0561-1. مؤرشف من الأصل في 2021-03-08.