|
تضامنًا مع حق الشعب الفلسطيني |
موشور (بصريات)
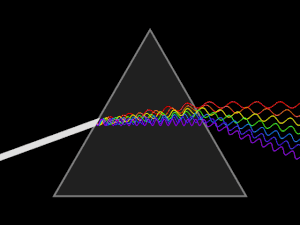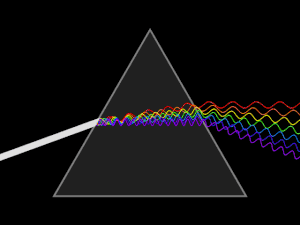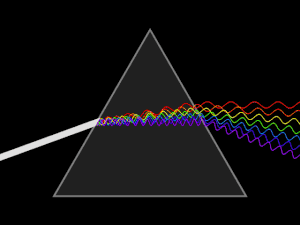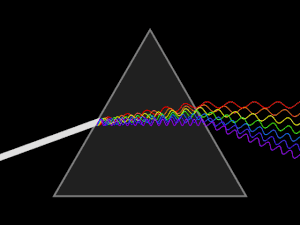
في البصريات الموشور أو المنشور هو وسط شفاف مثل الزجاج، محدود بوجهين مستويين يتقاطعان حسب مستقيم يسمى حرف الموشور، قاعدة الموشور هي الوجه المقابل للحرف.[1][2][3] زاوية الموشور (A) هي الزاوية المقابلة للقاعدة. ويرجع السبب في تحلل الضوء الأبيض إلى ألوانه المختلفة أثناء مروره داخل الموشور إلى اختلاف سرعة الضوء في مادة المنشور عن سرعته في الهواء. وهذا يؤدي إلى انكسار شعاع الضوء عند دخوله الوسط (الزجاج) بزوايا انكسار مختلفة، فيكون انكسار الضوء الأحمر أصغر من انكسار اللون الأزرق فينفصلا عن بعضهما (أنظر الشكل)، ويخرج الشعاعان الأحمر والأزرق من الموشور منفصلين. وحيث أن الضوء الأبيض مثل ضوء الشمس يحتوي على مجموعة من الألوان تشمل تحت الحمراء والحمراء والأصفر والأخضر بدرجاته والأزرق السماوي والأزرق بدرجاته إلى الأشعة البنفسجية وفوق البنفسجية، فأن جميع تلك الألوان الضوئية تنفصل عن بعضها البعض بفعل الموشور، لاختلاف معامل انكسار كل لون في الموشور، ونحصل على ما يسمى الطيف الضوئي.
يستخدم الموشور في عملية تحليل الضوء إلى ألوان الطيف (ألوان قوس قزح)، ونظراً لأن كل عنصر من العناصر الكيميائية له طيف ضوئي خاص به، مثل بصمة الإصبع بالنسبة للإنسان، ينبعث هذا الطيف الضوئي من العنصر عند إثارة ذراته بالحرارة العالية مثلا، يظهر بعد تحليله خلف الموشور على هيئة خطوط ضوئية متوازية، فيمكن عن طريق ذلك التعرف على العنصر.
معامل الانكسار

بفرض الموشور متماثل (على الأقل مثلث متساوي الساقين أو مثلث متساوي الأضلاع) وأن الشعاع الذي يحقق زاوية أقل انحراف يمر داخل الموشور موازياً لقاعدته ورأسه الزاوية ، يمكن اشتقاق العلاقة بدلالة معامل انكسار كل من الموشور والوسط خارج الموشور (عادة الهواء).
لإثبات ذلك سنفرض الموشور الموجود بالرسم المقابل. من الرسم نجد أن الشعاع الضوئي يسقط من D إلى A بزاوية ومن ثم ينكسر داخل المنشور مكوناً زاوية الانكسار وعليه يتحقق قانون الانكسار:
يمكن أيضا إثبات أن زاوية الانكسار تشكل نصف زاوية رأس المنشور في المثلث متساو الساقين. أحد الطرق لإثبات الأمر تكمن في تماثل زوايا المثلث وبإسقاط عمود من رأسه والذي بدوره ينصف زاوية الرأس نكون قد صنعنا مثلثا قائم الزاوية، يقطع امتداد الزاوية المنكسرة . الطريقة الأخرى تكمن في أن امتداد الزاويتين المنكسرتين سيشكل مع زاوية الرأس شكل رباعي دائري (لاحتوائه زاويتين متقابلتين قامتين هما العمودان الملونان بالأخضر). بالتالي يمكن كتابة العلاقة السابقة بالصورة:
مرة أخرى يكمل الشعاع المنكسر طريقه داخل الموشور موازيا للقاعدة ويخرج من الجانب الآخر عند النقطة B وينكسر مرة أخرى ماراً بالنقطة C. نظراً لتماثل المنشور، يمكننا تخيل العلاقة بشكل عكسي وإثبات زاوية انكساره عند الخروج هي أيضاً بينما كانت قبل الخروج شريطة أن معامل انكسار الوسط على الجانب الآخر هو نفسه معامل الانكسار على الطرف السابق قبل الدخول (أي أن الوسط خارج الموشور ثابت). لاحظ أيضاً أن:
وأن:
أي أن:
أو بعبارة أخرى
بتعويض هذه القيمة في قانون الانكسار مرة أخرى نجد أن:
اقرأ أيضا
مراجع
- ^ إف. جاي دوارتي and J. A. Piper (1982). "Dispersion theory of multiple-prism beam expanders for pulsed dye lasers". Opt. Commun. ج. 43 ع. 5: 303–307. Bibcode:1982OptCo..43..303D. DOI:10.1016/0030-4018(82)90216-4.
- ^ "The Discovery of the Spectrum of Light". مؤرشف من الأصل في 2017-12-29. اطلع عليه بتاريخ 2009-12-19.
- ^ Loenen, Nick (2012-02). Wooden Boat Building: How to Build a Dragon Class Sailboat (بEnglish). FriesenPress. ISBN:9781770974067. Archived from the original on 20 ديسمبر 2019.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ=(help)
| موشور في المشاريع الشقيقة: | |