|
تضامنًا مع حق الشعب الفلسطيني |
تفرد بي كي إل

تفرد بي كي إل (بالإنجليزية: Belinski-Khalatnikov-Lifshitz (BKL)) هو نموذج للتطور الديناميكي للكون بالقرب من تفرد الجاذبية الأولي، الموصوف بمحلول فوضوي متباين الخواص لمعادلة أينشتاين للجاذبية .[2] وفقًا لهذا النموذج، يتأرجح الكون بشكل فوضوي حول تفرد الجاذبية حيث يصبح الزمان والمكان مساويين للصفر. هذا التفرد حقيقي ماديًا بمعنى أنه خاصية ضرورية للحل، وسيظهر أيضًا في الحل الدقيق لتلك المعادلات. لم يتم إنشاء التفرد بشكل مصطنع من خلال الافتراضات والتبسيط التي تم إجراؤها بواسطة الحلول الخاصة الأخرى مثل حلول فريدمان - لوميتري - روبرتسون - ووكر وشبه الخواص وحلول كاسنر.
تم تسمية النموذج على اسم مؤلفيه فلاديمير بيلينسكي وإسحاق خالاتنيكوف وإيفجيني ليفشيتز، ثم عملوا في معهد لانداو للفيزياء النظرية .
تحتوي الصورة التي طورتها بي كي إل على عدة عناصر مهمة. وهذه هي:
- بالقرب من التفرد تطور الهندسة في نقطة مكانية مختلفة يفصل ذلك أن الحلول لل معادلات التفاضلية الجزئية يمكن أن يقترب من الحلول لل معادلات التفاضلية العادية فيما يتعلق الوقت لعوامل على نطاق والمكانية المحددة بشكل مناسب. وهذا ما يسمى تخمين بي كي إل.
- بالنسبة لمعظم أنواع المادة، يصبح تأثير حقول المادة على ديناميكيات الهندسة ضئيلًا بالقرب من التفرد. أو، على حد تعبير جون ويلر، "لا تهم المادة" بالقرب من التفرد. طرح عمل بي كي إل الأصلي تأثيرًا ضئيلًا لجميع المواد ولكنهم افترضوا لاحقًا أن "المادة الصلبة" (معادلة الحالة p = ε) المكافئة لحقل عددي عديم الكتلة يمكن أن يكون لها تأثير تعديل على الديناميكيات بالقرب من التفرد.
- تأتي المعادلات التفاضلية العادية التي تصف التقارب من فئة من الحلول المتجانسة مكانيًا والتي تشكل ديناميكيات مكسماستر : نموذج متذبذب وفوضوي معقد يعرض خصائص مشابهة لتلك التي ناقشها بي كي إل.
أصبحت دراسة ديناميات الكون في محيط التفرد الكوني مجالًا سريع التطور للفيزياء النظرية والرياضية الحديثة. إن تعميم نموذج بي كي إل على التفرد الكوني في النماذج الكونية متعددة الأبعاد ( نوع كلوزا- كلاين ) له طابع فوضوية في الزمكانات التي لا تزيد أبعادها عن عشرة، بينما في الزمان المكاني ذي الأبعاد الأعلى يكون الكون بعد خضوعه لعدد محدود من التذبذبات تدخل في نظام تعاقد رتيب من نوع كاسنر. [3] [4] [5]
كشف تطوير الدراسات الكونية القائمة على نماذج الأوتار الفائقة عن بعض الجوانب الجديدة للديناميكيات في محيط التفرد. [6] [7] [8] في هذه النماذج، لا يتم إثارة آليات تغيير حقبة كاسنر من خلال تفاعلات الجاذبية ولكن من خلال تأثير المجالات الأخرى الموجودة. ثبت أن النماذج الكونية المبنية على ستة نماذج من الأوتار الفائقة بالإضافة إلى نموذج الجاذبية الفائقة D = 11 تُظهر ديناميكيات بي كي إل الفوضوية تجاه التفرد. تم اكتشاف علاقة بين النماذج الكونية المتذبذبة الشبيهة بـ بي كي إل وفئة فرعية خاصة من جبر الكذب اللانهائي الأبعاد - ما يسمى بجبر كاك الزائدي - مودي. [9] [10] [11]
مقدمة
أساس علم الكونيات الحديث هو الحلول الخاصة لمعادلات مجال أينشتاين التي وجدها ألكسندر فريدمان في 1922-1924. يُفترض أن الكون متجانس (الفضاء له نفس الخصائص (المقاييس) المترية في جميع النقاط) ومتساوي الخواص (الفضاء له نفس المقاييس في جميع الاتجاهات). تتيح حلول فريدمان شكلين هندسيين محتملين للفضاء: نموذج مغلق بمساحة تشبه الكرة، منحنية للخارج (انحناء إيجابي ) ونموذج مفتوح مع مساحة تشبه السرج، منحنية إلى الداخل (انحناء سلبي ). في كلا النموذجين، لا يقف الكون ساكنًا، فهو إما يتوسع باستمرار (يصبح أكبر) أو يتقلص (يتقلص، ويصبح أصغر). وهذا ما أكده إدوين هابل الذي أسس انزياح هابل الأحمر للمجرات المتراجعة. الإجماع الحالي هو أن النموذج الخواص، بشكل عام، يعطي وصفًا مناسبًا للحالة الحالية للكون ؛ ومع ذلك، فإن الخواص في الكون الحالي بحد ذاته ليس سببًا لتوقع أنه كافٍ لوصف المراحل الأولى من تطور الكون . في الوقت نفسه، من الواضح أن التجانس في العالم الحقيقي، في أحسن الأحوال، مجرد تقريب. حتى لو كان بإمكان المرء التحدث عن توزيع متجانس لكثافة المادة على مسافات كبيرة مقارنة بالفضاء بين المجرات، فإن هذا التجانس يتلاشى عند المقاييس الأصغر. من ناحية أخرى، يذهب افتراض التجانس بعيدًا جدًا في الجانب الرياضي: فهو يجعل الحل متماثلًا للغاية والذي يمكن أن ينقل خصائص محددة تختفي عند النظر في حالة أكثر عمومية.
خاصية أخرى مهمة للنموذج الخواص هي الوجود الحتمي لتفرد الوقت : تدفق الوقت ليس مستمرًا، ولكنه يتوقف أو ينعكس بعد أن يصل الوقت إلى قيمة كبيرة جدًا أو صغيرة جدًا. بين التفردات، يتدفق الوقت في اتجاه واحد: بعيدًا عن التفرد ( سهم الوقت ). في النموذج المفتوح، يوجد تفرد لمرة واحدة، لذا يكون الوقت محدودًا في أحد طرفيه ولكنه غير محدود في الطرف الآخر، بينما في النموذج المغلق، هناك نوعان من التفردات التي تحدد الوقت عند كلا الطرفين ( الانفجار العظيم والأزمة الكبيرة ).
الخصائص الفيزيائية الوحيدة المثيرة للاهتمام للزمن المكاني (مثل التفردات) هي تلك الخصائص المستقرة، أي تلك الخصائص التي لا تزال تحدث عندما تكون البيانات الأولية مضطربة قليلاً. من الممكن أن تكون التفرد مستقرًا ولكنها ليست ذات فائدة مادية: الاستقرار ضروري ولكنه ليس شرطًا كافيًا للأهمية المادية. على سبيل المثال، يمكن أن يكون التفرد مستقرًا فقط في جوار مجموعات البيانات الأولية المقابلة لأكوان متباينة الخواص. نظرًا لأن الكون الفعلي يبدو الآن شبه متناحي الخواص، فإن مثل هذه التفرد لا يمكن أن تحدث في كوننا. الشرط الكافي ليكون التفرد المستقر ذا فائدة جسدية هو شرط أن تكون التفرد عامة (أو عامة). بشكل تقريبي، يكون التفرد المستقر عامًا إذا حدث بالقرب من كل مجموعة من الظروف الأولية وكانت الحقول غير الجاذبية مقيدة بطريقة معينة إلى الحقول "الواقعية فيزيائيًا" بحيث تكون معادلات أينشتاين، ومعادلات الحالة المختلفة، وما إلى ذلك، يفترض أنه يحتفظ بأزمنة الفضاء المتطورة. قد يحدث أن تكون التفرد مستقرًا في ظل اختلافات صغيرة في درجات الجاذبية الحقيقية للحرية، ومع ذلك فهي ليست عامة لأن التفرد يعتمد بطريقة ما على نظام الإحداثيات، أو بالأحرى على اختيار السطح الفائق الأولي الذي ينطلق منه الزمكان. يتطور.
بالنسبة لنظام المعادلات التفاضلية غير الخطية، مثل معادلات أينشتاين، لا يتم تحديد الحل العام بشكل لا لبس فيه. من حيث المبدأ، قد يكون هناك تكاملات عامة متعددة، وقد يحتوي كل منها على مجموعة فرعية محدودة فقط من جميع الشروط الأولية الممكنة. قد تحتوي كل من هذه التكاملات على جميع الوظائف المستقلة المطلوبة والتي، مع ذلك، قد تخضع لبعض الشروط (على سبيل المثال، بعض عدم المساواة ). لذلك، فإن وجود حل عام ذو تفرد لا يمنع وجود حلول عامة إضافية أخرى لا تحتوي على تفرد. على سبيل المثال، لا يوجد سبب للشك في وجود حل عام بدون تفرد يصف جسمًا منعزلًا بكتلة صغيرة نسبيًا.
من المستحيل العثور على جزء لا يتجزأ من جميع الأماكن وفي كل الأوقات. ومع ذلك، هذا ليس ضروريًا لحل المشكلة: يكفي دراسة الحل بالقرب من التفرد. وهذا من شأنه حل أيضا جانبا آخر للمشكلة: خصائص الزمكان المتري تطور في الحل العام عندما يصل إلى التفرد المادي، تفهم على أنها نقطة حيث كثافة المادة والثوابت لل انحناء ريمان الموتر تصبح لانهائية.
وجود تفرد للوقت المادي
كانت إحدى المشكلات الرئيسية التي درستها مجموعة لانداو (التي تنتمي إليها بي كي إل) هي ما إذا كانت النماذج الكونية النسبية تحتوي بالضرورة على فرادة زمنية أو ما إذا كانت فرادة الوقت هي قطعة أثرية من الافتراضات المستخدمة لتبسيط هذه النماذج. إن استقلال التفرد في افتراضات التناظر يعني أن فرادات الوقت لا توجد فقط في الخاص، ولكن أيضًا في الحلول العامة لمعادلات أينشتاين. من المعقول أن نقترح أنه في حالة وجود مفردة في الحل العام، يجب أن تكون هناك بعض المؤشرات التي تستند فقط إلى الخصائص الأكثر عمومية لمعادلات أينشتاين، على الرغم من أن هذه المؤشرات في حد ذاتها قد تكون غير كافية لوصف التفرد.
معيار عمومية الحلول هو عدد وظائف إحداثيات الفضاء المستقلة التي تحتوي عليها. وتشمل هذه الوظائف "المستقلة جسديًا" فقط والتي لا يمكن تقليل عددها بأي اختيار للإطار المرجعي . في الحل العام، يجب أن يكون عدد هذه الوظائف كافيًا لتعريف الشروط الأولية بشكل كامل (توزيع المادة وحركتها، وتوزيع مجال الجاذبية ) في لحظة معينة من الوقت يتم اختيارها كأولوية. هذا الرقم هو أربعة لمساحة فارغة (فراغ)، وثمانية لمادة و / أو مساحة مملوءة بالإشعاع.[12][13]
عمل سابق لمجموعة لانداو ؛ [14] [15] [16] تمت مراجعته في [12] ) أدى إلى استنتاج مفاده أن الحل العام لا يحتوي على تفرد مادي. تم إجراء هذا البحث عن فئة أوسع من الحلول ذات التفرد، بشكل أساسي، من خلال طريقة التجربة والخطأ، نظرًا لعدم وجود نهج منهجي لدراسة معادلات أينشتاين. النتيجة السلبية، التي يتم الحصول عليها بهذه الطريقة، ليست مقنعة بحد ذاتها ؛ الحل بالدرجة اللازمة من العمومية من شأنه أن يبطله، وفي نفس الوقت سيؤكد أي نتائج إيجابية تتعلق بالحل المحدد.
في ذلك الوقت، كان المؤشر الوحيد المعروف لوجود التفرد المادي في الحل العام مرتبطًا بشكل معادلات آينشتاين المكتوبة في إطار متزامن، أي في إطار يتم فيه مزامنة الوقت المناسب x 0 = t في جميع أنحاء الفضاء ؛ في هذا الإطار، يكون عنصر المسافة الفضائية dl منفصلاً عن الفاصل الزمني dt .[note 1] معادلة اينشتاين
-
(eq. 1)
مكتوبًا في إطار متزامن يعطي نتيجة يصبح فيها المحدد المتري g حتمًا صفرًا في وقت محدد بغض النظر عن أي افتراضات حول توزيع المادة.[12][13]
ومع ذلك، فإن الجهود المبذولة لإيجاد التفرد المادي العام قد تم التخلي عنها بعد أن أصبح من الواضح أن التفرد المذكور أعلاه مرتبط بخاصية هندسية محددة للإطار المتزامن: عبور إحداثيات الخط الزمني. يحدث هذا التقاطع على بعض الأسطح الفوقية المحاطة وهي نظائر رباعية الأبعاد للأسطح الكاوية في البصريات الهندسية ؛ يصبح g صفرًا بالضبط عند هذا التقاطع.[16] لذلك، على الرغم من أن هذه التفردية عامة، إلا أنها خيالية وليست مادية ؛ يختفي عند تغيير الإطار المرجعي. هذا، على ما يبدو، أقنع الباحثين بإجراء مزيد من التحقيقات على هذا المنوال.
مرت عدة سنوات قبل أن يتجلى الاهتمام بهذه المشكلة مرة أخرى عندما نشر بنروز بعام 1965 نظرياته التي ربطت بين وجود تفرُّد ذات طابع غير معروف مع بعض الافتراضات العامة جدًا التي لم يكن لديها أي شيء مشترك مع اختيار الإطار المرجعي. تم العثور على نظريات أخرى مماثلة في وقت لاحق من قبل هوكينج [17] [18] وجيروتش [19] (انظر نظريات بينروز - هوكينغ التفرد ). أدى هذا إلى إحياء الاهتمام بالبحث عن حلول فردية.
محلول متجانس معمم
في مساحة متجانسة وخواص الخواص، يتم تحديد المقياس تمامًا، تاركًا مجانًا فقط علامة الانحناء. بافتراض تجانس المساحة فقط مع عدم وجود تناظر إضافي مثل الخواص، يترك قدرًا أكبر من الحرية في اختيار المقياس. يتعلق ما يلي بالجزء المكاني من المقياس في لحظة معينة من الوقت t بافتراض إطار متزامن بحيث يكون t هو نفس الوقت المتزامن للمساحة بأكملها.
تخمين بي كي إل
في عملهم عام 1970، [2] ذكر بي كي إل أنه عندما يقترب المرء من التفرد، فإن المصطلحات التي تحتوي على مشتقات زمنية في معادلات أينشتاين تهيمن على تلك التي تحتوي على المشتقات المكانية . عُرف هذا منذ ذلك الحين باسم تخمين بي كي إل ويشير إلى أن المعادلات التفاضلية الجزئية لأينشتاين (PDE) يتم تقريبها جيدًا بواسطة المعادلات التفاضلية العادية (ODEs)، ومن هنا تصبح ديناميكيات النسبية العامة محلية ومتذبذبة بشكل فعال. يتم تقريب التطور الزمني للحقول في كل نقطة مكانية جيدًا بواسطة علم الكونيات المتجانسة في تصنيف بيانكي.
من خلال فصل مشتقات الوقت والمكان في معادلات أينشتاين، على سبيل المثال، بالطريقة المستخدمة أعلاه لتصنيف المساحات المتجانسة، ثم تحديد المصطلحات التي تحتوي على مشتقات فضائية تساوي الصفر، يمكن للمرء تحديد ما يسمى بالنظرية المقطوعة لـ نظام (معادلات مبتورة).[20] بعد ذلك، يمكن جعل تخمين بي كي إل أكثر تحديدًا:
التخمين الضعيف : مع اقتراب التفرد، فإن المصطلحات التي تحتوي على مشتقات الفضاء في معادلات أينشتاين لا تكاد تذكر مقارنة بالمصطلحات التي تحتوي على مشتقات زمنية. وهكذا، عندما يتم الاقتراب من التفرد، تقترب معادلات أينشتاين من تلك التي تم العثور عليها عن طريق تعيين شروط مشتقة إلى الصفر. وهكذا، فإن التخمين الضعيف يقول أن معادلات أينشتاين يمكن تقريبها جيدًا من خلال المعادلات المقطوعة في جوار التفرد. لاحظ أن هذا لا يعني أن حلول معادلات الحركة الكاملة ستقترب من حلول المعادلات المقطوعة مع اقتراب التفرد. تم التقاط هذا الشرط الإضافي في الإصدار القوي على النحو التالي.
تخمين قوي : مع اقتراب التفرد، تقترب معادلات أينشتاين من نظريتها المقتطعة بالإضافة إلى أن حلول المعادلات الكاملة تقترب جيدًا من خلال حلول المعادلات المقطوعة.
في البداية، بدا أن تخمين بي كي إل يعتمد على التنسيق وغير قابل للتصديق إلى حد ما.[21] [22] فعلى سبيل المثال من بين الانتقادات العشرة لدراسات بي كي إل، يتضمن الاختيار غير المناسب وفقًا لبارو وتيبلير للإطار المتزامن كوسيلة لفصل مشتقات الزمان والمكان. تم إعادة صياغة حدسية بي كي إل في بعض الأحيان في الأدبيات كبيان أنه بالقرب من التفرد فقط مشتقات الوقت مهمة. مثل هذا البيان، المأخوذ بالقيمة الاسمية، خاطئ أو مضلل في أفضل الأحوال لأنه، كما هو موضح في تحليل بي كي إل نفسه، لا يمكن إهمال التدرجات الشبيهة بالفضاء للموتر المتري للحلول العامة لجاذبية أينشتاين الصافية في أبعاد الزمكان الأربعة، وفي تلعب الحقيقة دورًا مهمًا في ظهور النظام التذبذب. ومع ذلك، توجد إعادة صياغة لنظرية أينشتاين من حيث المتغيرات الجديدة التي تتضمن التدرجات ذات الصلة، على سبيل المثال في المتغيرات الشبيهة بأشتيكار، والتي يكون فيها بيان الدور المهيمن لمشتقات الوقت صحيحًا.[20] صحيح أن المرء يحصل في كل نقطة مكانية على وصف فعال للتفرد من حيث النظام الديناميكي ذي الأبعاد المحدودة الموصوف بواسطة المعادلات التفاضلية العادية فيما يتعلق بالوقت، لكن التدرجات المكانية تدخل هذه المعادلات بشكل غير تافه.
أظهر التحليل اللاحق الذي أجراه عدد كبير من المؤلفين أن تخمين بي كي إل يمكن أن يكون دقيقًا والآن هناك مجموعة رائعة من الأدلة العددية والتحليلية التي تدعمها.[23] من الإنصاف القول إننا ما زلنا بعيدين تمامًا عن إثبات التخمين القوي. ولكن كان هناك تقدم ملحوظ في نماذج أبسط. على وجه الخصوص، أظهر بيرجر وجارفينكل ومونكريف وإيزنبرج وويفر وآخرون أنه في فئة من النماذج، مع اقتراب التفرد، تقترب حلول معادلات مجال أينشتاين الكاملة من "مصطلح السرعة المسيطر" (المقطوع) التي تم الحصول عليها بواسطة إهمال المشتقات المكانية.[23] [24] [25] [26] [27] أظهر أندرسون وريندال [28] أنه بالنسبة للجاذبية المقترنة بحقل عددي عديم الكتلة أو سائل صلب، لكل حل للمعادلات المقطوعة يوجد حل كامل معادلات المجال التي تتقارب مع الحل المبتور مع اقتراب التفرد، حتى في حالة عدم وجود تماثلات. تم تعميم هذه النتائج لتشمل أيضًا حقول قياس النموذج p. [29] في هذه النماذج المبتورة، تكون الديناميكيات أبسط، مما يسمح ببيان دقيق للتخمين يمكن إثباته. في الحالة العامة، يأتي أقوى دليل حتى الآن من التطورات العددية. بدأ بيرغر ومونكريف [30] برنامجًا لتحليل التفردات الكونية العامة. بينما ركز العمل الأولي على حالات التناظر المخفّضة، [31] مؤخرًا، [32] تطورًا عدديًا لأزمنة الزمكان مع عدم وجود تماثلات يظهر فيها سلوك مكسماستر مرة أخرى. أخيرًا، جاء دعم إضافي للتخمين من دراسة عددية لسلوك حقول الاختبار بالقرب من تفرد ثقب أسود شوارزشيلد. [33]
حل كاسنر

يبدأ نهج بي كي إل للمساحات المتجانسة (على عكس الخواص) بتعميم حل معين دقيق مشتق من كاسنر [34] لحقل في الفراغ، يكون فيه الفراغ متجانسًا وله مقياس إقليدي يعتمد على الوقت وفقًا لمقياس كاسنر.
-
(eq. 2)
( dl هو عنصر الخط ؛ dx، dy، dz هي عمليات نزوح متناهية الصغر في الأبعاد المكانية الثلاثة، و t هي الفترة الزمنية التي مرت منذ بعض اللحظات الأولية t 0 = 0). هنا، p 1، p 2، p 3 هي أي ثلاثة أرقام تفي بشروط كاسنرالتالية
-
(eq. 3)
بسبب هذه العلاقات، يكون رقم واحد فقط من الأعداد الثلاثة مستقلًا ( معادلتان بثلاثة مجاهيل ). جميع الأرقام الثلاثة ليست هي نفسها أبدًا ؛ رقمان متماثلان فقط في مجموعات القيم
و (0، 0، 1). [note 3] في جميع الحالات الأخرى، تكون الأرقام مختلفة، رقم واحد سلبي والآخران موجبان. تم إثبات ذلك جزئيًا من خلال تربيع جانبي الشرط الأول eq. 3 و تطوير الساحة:
المصطلح يساوي 1 عن طريق الشرط الثاني eq. 3 وبالتالي يجب أن يكون المصطلح مع حاصل الضرب المختلط صفرًا. هذا ممكن إذا كانت واحدة على الأقل من p 1 و p 2 و p 3 سالبة.
إذا تم ترتيب الأرقام بترتيب تصاعدي، p 1 < p 2 < p 3، فإنها تتغير في الفترات (الشكل 4)
-
(eq. 4)

مقياس كاسنر eq. 2 يتوافق مع مساحة مسطحة متجانسة ولكن متباينة الخواص حيث تزداد جميع الأحجام بمرور الوقت بطريقة تزيد فيها المسافات الخطية على محورين y و z بينما تقل المسافة على طول المحور x. تسبب اللحظة t = 0 تفردًا في الحل ؛ لا يمكن تجنب التفرد في المقياس عند t = 0 بواسطة أي تحويل للإطار المرجعي. عند التفرد، تذهب ثوابت موتر الانحناء رباعي الأبعاد إلى اللانهاية. الاستثناء هو الحالة p 1 = р 2 = 0، р 3 = 1 ؛ تتوافق هذه القيم مع الزمكان المسطح: التحويل t sh z = ζ، t ch z = τ يحول مقياس كاسنر ( eq. 2 ) إلى تحويل جاليليو.
معامل بي كي إل المتغير في التجربة بأرقام P1، P 2، P 3، وكمعامل واحد مستقل وحقيقي معامل u (ليفشيتز - خالاتنيكوف [35] ) على النحو التالي:
-
(eq. 5)
تبدو معلمات مؤشر كاسنر غامضة حتى يفكر المرء في القيدين على المؤشرات eq. 3 . يعمل كلا القيدان على إصلاح المقياس العام للمؤشرات بحيث يمكن أن تختلف نسبها فقط. من الطبيعي اختيار إحدى هذه النسب كمعامل جديد، والذي يمكن القيام به بست طرق مختلفة. انتقاء u = u 32 = p 3 / p 2، على سبيل المثال، من السهل التعبير عن جميع النسب الست الممكنة بدلالة ذلك. حذف p 3 = up 2 أولاً، ثم استخدام القيد الخطي لإزالة p 1 = 1 - p 2 - up 2 = 1 - (1 + u ) p 2، يقلل القيد التربيعي إلى معادلة من الدرجة الثانية في p 2.
-
(eq. 5a)
مع الجذور p 2 = 0 (واضح) و p 2 = (1 + u ) / (1 + u + u 2 )، ومن ثم يتم الحصول على p 1 و p 3 بالتعويض العكسي . يمكن للمرء تحديد ستة من هذه المعلمات u ab = p a / p b، والتي لها p c ≤ p b ≤ p a عندما ( c، b، a ) هي تبديل دوري لـ (1، 2، 3). [36] يتم الحصول على جميع القيم المختلفة لـ p 1 و p 2 و p 3 مرتبة على النحو الوارد أعلاه مع تشغيل u في النطاق u ≥ 1. يتم إحضار القيم u <1 في هذا النطاق وفقًا لـ
-
(eq. 6)
في الحل المعمم، الشكل المقابل لـ eq. 2 ينطبق فقط على المقياس المقارب (المقياس القريب من التفرد t = 0)، على التوالي، على الشروط الرئيسية لتوسعه المتسلسل بواسطة قوى t . في الإطار المرجعي المتزامن يتم كتابته في شكل eq. 1 مع عنصر مسافة المسافة
-
(eq. 7)
حيث v = l [ mn ]. من المناسب إدخال الكميات التالية [note 4]
-
(eq. 8)
تحدد المتجهات ثلاثية الأبعاد l، m، n الاتجاهات التي تتغير فيها مسافة الفضاء بمرور الوقت بواسطة قوانين القوة eq. 8 . هذه المتجهات، وكذلك الأرقام p l، p m، p n التي، كما كان من قبل، مرتبطة بـ eq. 3، هي وظائف إحداثيات الفضاء. القوى p l، p m، p n ليست مرتبة بترتيب تصاعدي، مع الاحتفاظ بالرموز p 1، p 2، p 3 للأرقام في eq. 5 التي تبقى مرتبة بترتيب تصاعدي. محدد مقياس eq. 7 هو
-
(eq. 9)
حيث v = l [mn]. من الملائم إدخال الكميات التالية [note 5]
-
(eq. 10)
مقياس الفضاء في eq. 7 متباين الخواص لأن قوى t في eq. 8 لا يمكن أن يكون لها نفس القيم. عند الاقتراب من التفرد عند t = 0، تنخفض المسافات الخطية في كل عنصر فضائي في اتجاهين وتزداد في الاتجاه الثالث. حجم العنصر يتناسب مع t .
يتم تقديم مقياس كاسنر في معادلات أينشتاين عن طريق استبدال موتر القياس المتري γ αβ من eq. 7 دون تحديد مسبق، تبعية a، b، c من t :[note 6]
حيث تشير النقطة الموجودة فوق الرمز إلى التمايز فيما يتعلق بالوقت. معادلة آينشتاين eq. 11 تأخذ الشكل
-
(eq. 14)
جميع شروطه هي من الدرجة الثانية للكمية الكبيرة (عند t → 0) 1 / t . في معادلات أينشتاين، eq. 12، تظهر شروط هذا الطلب فقط من المصطلحات المتباينة زمنيًا. إذا لم تتضمن مكونات P αβ شروط ترتيب أعلى من اثنين، إذن
-
(eq. 15)
حيث تحدد المؤشرات l، m، n مكونات الموتر في الاتجاهات l، m، n .[12] هذه المعادلات مع eq. 14 أعط التعبيرات eq. 8 مع القوى التي ترضي eq. 3. ومع ذلك، فإن وجود قوة سالبة واحدة بين القوى الثلاث p l، p m، p n ينتج عنه ظهور مصطلحات من P αβ بترتيب أكبر من t −2 . إذا كانت القدرة السالبة هي p l ( p l = p 1 <0)، فإن P αβ تحتوي على دالة الإحداثيات λ و eq. 12 يصبح
-
(eq. 16)
هنا، المصطلحات الثانية من الترتيب t −2 ( p m + p n - p l ) حيث p m + p n - p l = 1 + 2 | ص ل | > 1. [note 7] لإزالة هذه الشروط واستعادة eq. 7، من الضروري فرض الشرط λ = 0 على وظائف الإحداثيات.
معادلات أينشتاين الثلاثة المتبقية eq. 13 تحتوي فقط على مشتقات الوقت من الدرجة الأولى للموتر المتري. إنها توفر ثلاث علاقات مستقلة عن الوقت يجب فرضها حسب الشروط الضرورية على وظائف التنسيق في eq. 7 . هذا، مع الشرط λ = 0، يجعل أربعة شروط. تربط هذه الشروط عشر وظائف إحداثيات مختلفة: ثلاثة مكونات لكل من المتجهات l، m، n، ووظيفة واحدة في قوى t (أي من الدوال p l، p m، p n، المرتبطة بالشروط eq. 3 ). عند حساب عدد الوظائف التعسفية جسديًا، يجب أن يؤخذ في الاعتبار أن النظام المتزامن المستخدم هنا يسمح بتحولات عشوائية مستقلة عن الوقت للإحداثيات الفضائية الثلاثة. لذلك، يحتوي الحل النهائي على إجمالي 10 - 4 - 3 = 3 وظائف اعتباطية فيزيائية وهي أقل بواحد مما هو مطلوب للحل العام في الفراغ.
لا يتم التقليل من درجة العمومية التي تم التوصل إليها في هذه المرحلة من خلال إدخال المادة ؛ تتم كتابة المادة في eq. 7 ويساهم بأربع وظائف إحداثية جديدة ضرورية لوصف التوزيع الأولي لكثافته والمكونات الثلاثة لسرعته. هذا يجعل من الممكن تحديد تطور المادة فقط من قوانين حركتها في مجال الجاذبية المعطى مسبقًا وهو المعادلات الهيدروديناميكية.
-
(eq. 17)
-
(eq. 18)
حيث u i هي السرعة رباعية الأبعاد، ε و هي كثافات الطاقة وانتروبيا المادة (راجع [37] و ؛ [38] أيضًا ؛ [39] للحصول على التفاصيل، انظر [40] ). بالنسبة للمعادلة الفائقة الصغر للحالة p = ε / 3 الانتروبيا σ ~ ε 1/4 . المصطلحات الرئيسية في eq. 17 eq. 18 هي تلك التي تحتوي على مشتقات زمنية. من eq. 17 ومكونات الفضاء من eq. 18 واحد لديه
فينتج،
-
(eq. 19)
حيث "const" هي كميات لا تعتمد على الوقت. بالإضافة إلى ذلك، من الهوية u i u i = 1 واحد لديه (لأن جميع المكونات المتغيرة لـ u α لها نفس الترتيب)
حيث u n هي مكون السرعة على طول اتجاه n المرتبط بأعلى قوة (موجبة) لـ t (بافتراض أن p n = p 3 ). من العلاقات المذكورة أعلاه، يتبع ذلك
-
(eq. 20)
أو
-
(eq. 21)
يمكن استخدام المعادلات أعلاه لتأكيد أن مكونات المادة موتر الإجهاد-الطاقة-الزخم يقف في الجانب الأيمن من المعادلات
هي، في الواقع، إلى ترتيب أقل بمقدار 1 / t من الشروط الرئيسية في الجانب الأيسر. في المعادلات يؤدي وجود الأمر فقط إلى تغيير العلاقات المفروض على وظائف التنسيق المكونة لها.[12]
حقيقة أن ε تصبح لانهائية بموجب القانون eq. 21 يؤكد أن في حل eq. 7 يتعامل المرء مع التفرد المادي عند أي قيم للقوى p 1، p 2، p 3 باستثناء (0، 0، 1). بالنسبة لهذه القيم الأخيرة، تكون التفرد غير مادية ويمكن إزالتها عن طريق تغيير الإطار المرجعي.
تنشأ التفرد الخيالي المطابق للقوى (0، 0، 1) نتيجة عبور إحداثيات الخط الزمني فوق بعض " السطح البؤري " ثنائي الأبعاد. كما هو [12] يمكن دائمًا اختيار إطار مرجعي متزامن بطريقة تجعل هذا الخط الزمني الحتمي يحدث بالضبط على هذا السطح (بدلاً من سطح كاوي ثلاثي الأبعاد). لذلك، يجب أن يوجد حل بهذا الشكل المتزامن لكامل التفرد الخيالي للفضاء مع مجموعة كاملة من الوظائف التعسفية اللازمة للحل العام. بالقرب من النقطة t = 0، فإنه يسمح بالتمدد المنتظم بواسطة قوى t الكاملة. لتحليل هذه الحالة، انظر. [41]
الوضع المتذبذب نحو التفرد
الحل العام بالتعريف مستقر تمامًا ؛ وإلا لما كان الكون موجودًا. أي اضطراب يعادل تغيير في الظروف الأولية في وقت ما ؛ نظرًا لأن الحل العام يسمح بشروط أولية عشوائية، فإن الاضطراب غير قادر على تغيير طابعه. بالنظر إلى هذه الزاوية، فإن الشروط الأربعة المفروضة على وظائف الإحداثيات في الحل eq. 7 أنواع مختلفة: ثلاثة شروط تنشأ من المعادلات = 0 هي "طبيعية" ؛ هم نتيجة لهيكل معادلات آينشتاين. ومع ذلك، فإن الشرط الإضافي λ = 0 الذي يتسبب في فقدان وظيفة مشتقة واحدة، هو من نوع مختلف تمامًا: عدم الاستقرار الناجم عن الاضطرابات يمكن أن يكسر هذا الشرط. يجب أن يؤدي عمل هذا الاضطراب إلى إحضار النموذج إلى وضع آخر أكثر عمومية. لا يمكن اعتبار الاضطراب صغيراً: الانتقال إلى وضع جديد يتجاوز نطاق الاضطرابات الصغيرة جدًا.
يحدد تحليل سلوك النموذج تحت تأثير الاضطراب، الذي أجرته بي كي إل، وضعًا تذبذبًا معقدًا عند الاقتراب من التفرد.[2] [42] [43][44] لم يتمكنوا من إعطاء كل التفاصيل عن هذا الوضع في الإطار العريض للحالة العامة. ومع ذلك، أوضح بي كي إل أهم خصائص وخصائص الحل على نماذج محددة تسمح بدراسة تحليلية بعيدة المدى.
تعتمد هذه النماذج على مقياس فضاء متجانس من نوع معين. إن افتراض تجانس المساحة دون أي تناظر إضافي يترك حرية كبيرة في اختيار المقياس. يتم تصنيف جميع المساحات المتجانسة الممكنة (ولكن متباينة الخواص)، وفقًا لبيانكي، في عدة أنواع بيانكي (من النوع الأول إلى التاسع) . [45] (انظر أيضًا الحل المتجانس المعمم ) يبحث بي كي إل فقط في مساحات من أنواع بيانكي الثامن والتاسع.
إذا كان المقياس على شكل eq. 7 الشكل 7، لكل نوع من المساحات المتجانسة توجد علاقة وظيفية بين المتجهات المرجعية l و m و n وإحداثيات الفضاء. الشكل المحدد لهذه العلاقة ليس مهما. الحقيقة المهمة هي أنه بالنسبة للمسافات من النوع الثامن والتاسع، فإن الكميات λ و μ و ν eq. 10 عبارة عن ثوابت بينما جميع المنتجات "المختلطة" l rot m و l rot n و m rot l وما إلى ذلك . هي أصفار. بالنسبة للمسافات من النوع IX، فإن الكميات λ و μ و لها نفس العلامة ويمكن للمرء أن يكتب λ = μ = ν = 1 (تغيير الإشارة المتزامن للثوابت الثلاثة لا يغير شيئًا). بالنسبة للمسافات من النوع VIII، يكون للثوابتين إشارة معاكسة لعلامة الثابت الثالث ؛ يمكن للمرء أن يكتب، على سبيل المثال، λ = - 1، μ = ν = 1. [note 8]
وبالتالي تقتصر دراسة تأثير الاضطراب على "وضع كاسنر" على دراسة تأثير المصطلحات المحتوية على λ في معادلات أينشتاين. تعد الفراغات من النوع الثامن والتاسع أكثر النماذج ملاءمة لمثل هذه الدراسة. نظرًا لأن جميع الكميات الثلاثة λ و μ و في أنواع بيانكي هذه تختلف عن الصفر، فإن الشرط λ = 0 لا ينطبق بغض النظر عن الاتجاه l، m، n له اعتماد سالب على وقت قانون الطاقة.
معادلات أينشتاين للنماذج الفضائية من النوع الثامن والنوع التاسع هي [46] [note 9]
-
(eq. 22)
-
(eq. 23)
(المكونات المتبقية
و
و
و
و
و
هي أصفار متطابقة). تحتوي هذه المعادلات على وظائف الوقت فقط ؛ هذا شرط يجب الوفاء به في جميع المساحات المتجانسة. هنا، eq. 22 eq. 23 دقيقة ولا تعتمد صحتها على مدى قرب المرء من التفرد عند t = 0. [note 10] مشتقات الوقت في eq. 22 eq. 23 تتخذ شكلًا أبسط إذا تم استبدال а، b، с باللوغاريتمات α، β، γ:
-
(eq. 24)
استبدال المتغير t بـ وفقًا لما يلي:
-
(eq. 25)
ثم (تشير الرموز الفرعية إلى التمايز بواسطة τ):
-
(eq. 26)
-
(eq. 27)
جمع المعادلات معا eq. 26 والتعويض في الجانب الأيسر بالمجموع (α + β + γ) τ τ وفقًا eq. 27 الشكل 27، يحصل المرء على معادلة تحتوي فقط على المشتقات الأولى والتي تعد أول تكامل للنظام eq. 26 :
-
(eq. 28)
تلعب هذه المعادلة دور الشرط الملزم المفروض على الحالة الأولية eq. 26 . وضع كاسنر eq. 8 هو حل eq. 26 عند تجاهل كل الحدود في الجانب الأيمن. لكن مثل هذا الموقف لا يمكن أن يستمر (عند t → 0) إلى أجل غير مسمى لأنه من بين هذه المصطلحات يوجد دائمًا بعض تلك التي تنمو. وبالتالي، إذا كانت القدرة السالبة في الوظيفة a ( t ) ( p l = p 1 )، فإن اضطراب وضع كاسنر سينشأ عن المصطلحات λ 2 a 4 ؛ ستنخفض بقية الشروط مع تناقص t . إذا تم ترك شروط النمو فقط في الجانب الأيمن من eq. 26، يحصل المرء على النظام:
-
(eq. 29)
(قارن eq. 16 ؛ أدناه يتم استبداله λ 2 = 1). يجب أن يصف حل هذه المعادلات التطور المتري من الحالة الأولية، حيث يتم وصفه بواسطة eq. 8 مع مجموعة معينة من القوى (مع p l <0) ؛ دع p l = р 1، p m = р 2، p n = р 3 بحيث
-
(eq. 30)
ثم
-
(eq. 31)
حيث Λ ثابت. الشروط الأولية eq. 29 يتم إعادة تعريف eq. 29
-
(eq. 32)
المعادلات eq. 29 مندمجة بسهولة ؛ الحل الذي يفي بشرط eq. 32 هو
-
(eq. 33)
حيث b 0 و c 0 هما ثابتان إضافيتان.
يمكن بسهولة ملاحظة أن تقارب الوظائف eq. 33 في t → 0 يساوي eq. 30 . التعبيرات المقاربة لهذه الوظائف والوظيفة t (τ) في τ → −∞ هي [note 11]
التعبير عن a، b، c كوظائف لـ t، يكون بـ
-
(eq. 34)
حيث
-
(eq. 35)
ثم
يوضح ما سبق أن الاضطراب يعمل بطريقة تجعله يغير أحد أوضاع Kasner مع وضع Kasner آخر، وفي هذه العملية تنقلب القوة السلبية لـ t من الاتجاه l إلى الاتجاه m : إذا كانت قبل ذلك p l <0، فهي الآن كذلك ص ' م <0. أثناء هذا التغيير، تمر الوظيفة a ( t ) عبر الحد الأقصى و b ( t ) يمر عبر الحد الأدنى ؛ ب، الذي كان يتناقص من قبل، يزداد الآن: أ من الزيادة يصبح تناقصًا ؛ ونقص c ( t ) يتناقص أكثر. الاضطراب نفسه (λ 2 a 4α في eq. 29 )، والذي كان يتزايد من قبل، يبدأ الآن في الانخفاض ويموت. يؤدي التطور الإضافي بالمثل إلى زيادة الاضطراب من الشروط مع μ 2 (بدلاً من λ 2 ) في eq. 26، التغيير التالي لوضع كاسنر، وهكذا.
من الملائم كتابة قاعدة استبدال الطاقة eq. 35 بمساعدة البارامترات eq. 5 :
-
(eq. 37)
تظل القوة الأكبر من القوتين الموجبتين موجبة.
يطلق بي كي إل على هذا الانقلاب في القوة السلبية بين الاتجاهات حقبة كاسنر . إن المفتاح لفهم طبيعة التطور المتري عند الاقتراب من التفرد هو بالضبط عملية تناوب حقبة كاسنر مع تقليب القوى p l، p m، p n بواسطة القاعدة eq. 37.
التناوب المتتالية eq. 37 مع قلب القوة السالبة p 1 بين الاتجاهين l و m (فترة كاسنر) يستمر باستنفاد الجزء الكامل من u الأولي حتى اللحظة التي تكون فيها u <1. تتحول القيمة u <1 إلى u > 1 وفقًا لـ eq. 6 ؛ في هذه اللحظة القوة السالبة هي p l أو p m بينما p n تصبح الأصغر من رقمين موجبين ( p n = p 2 ). السلسلة التالية من عهود كاسنر تقلب القوة السالبة بين الاتجاهين n و l أو بين n و m . عند القيمة الأولية التعسفية ( غير المنطقية ) لـ u تستمر عملية التناوب هذه غير محدودة. [note 12]
في الحل الدقيق لمعادلات أينشتاين، تفقد القوى p l، p m، p n معناها الأصلي الدقيق. هذا الظرف يقدم بعض "غموض" في تحديد هذه الأرقام (ومعهم، إلى المعلمة ش) التي، وإن كانت صغيرة، يجعل معنى تحليل أي (على سبيل المثال، محددة عقلانية ) قيم ش. لذلك، فقط هذه القوانين التي تهم التعسفي القيم غير المنطقية من ش لها أي معنى خاص.
الفترات الأكبر التي تتأرجح فيها مقاييس المسافات الفضائية على محورين بينما تتناقص المسافات على طول المحور الثالث بشكل رتيب، تسمى العصور ؛ تقل الأحجام بقانون قريب من ~ ر . عند الانتقال من عصر إلى آخر، ينقلب الاتجاه الذي تتناقص فيه المسافات بشكل رتيب من محور إلى آخر. يكتسب ترتيب هذه التحولات الصفة المقاربة لعملية عشوائية . نفس الترتيب العشوائي هو أيضًا سمة من سمات تناوب أطوال العصور المتتالية (حسب طول العصر، تفهم بي كي إل عدد حقبة كاسنر التي تحتوي عليها العصر، وليس الفاصل الزمني).
لكل حقبة تتوافق مع سلسلة من قيم المعامل u بدءًا من الأعظم،
ومن خلال القيم
- 1،
- 2، ...، الوصول إلى الأصغر،
<1. ثم
-
(eq. 41)
أي أن k ( s) = [
] حيث تعني الأقواس الجزء الكامل من القيمة. الرقم k ( s ) هو طول العصر، ويقاس بعدد فترات كاسنر التي تحتوي عليها تلك الحقبة للعصر القادم.
-
(eq. 42)
في السلسلة اللامحدودة من الأرقام u، التي تتكون من هذه القواعد، توجد قيم صغيرة متناهية الصغر (ولكن ليست صفرية أبدًا) x ( s ) وأطوال كبيرة بشكل غير محدود بالمقابل k ( s ) .
تصبح سلسلة العصر أكثر كثافة عند الاقتراب من t = 0. ومع ذلك، فإن المتغير الطبيعي لوصف المسار الزمني لهذا التطور ليس الوقت العالمي t، ولكن لوغاريتمه، ln t، والذي من خلاله يتم تمديد العملية الكاملة للوصول إلى التفرد إلى −∞.
حسب eq. 33، إحدى الوظائف أ، ب، ج، التي تمر بحد أقصى أثناء الانتقال بين فترات كاسنر، في ذروة الحد الأقصى لها هي
-
(eq. 38)
حيث من المفترض أن الحد الأقصى هو كبير مقارنة ب 0 ج 0؛ في eq. 38 u هي قيمة المعلمة في حقبة كاسنر قبل الانتقال. يمكن أن نرى من هنا أن قمم الحدود القصوى المتتالية خلال كل عصر تنخفض تدريجياً. في الواقع، في حقبة كاسنر التالية، يكون لهذه المعلمة القيمة u ' = u - 1، ويتم استبدال Λ وفقًا لـ eq. 36 مع Λ '= Λ (1-2 | ص 1 ( ش ) |). لذلك، فإن نسبة 2 حد أقصى متتالي هي
وأخيراً
-
(eq. 39)
ما سبق حلول لمعادلات أينشتاين في الفراغ. أما بالنسبة لصيغة كاسنر الخالصة، فإن الأمر لا يغير الخصائص النوعية لهذا الحل ويمكن كتابته فيه بغض النظر عن رد فعله على الميدان. ومع ذلك، إذا فعل المرء هذا للنموذج قيد المناقشة، والذي يُفهم على أنه حل دقيق لمعادلات أينشتاين، فإن الصورة الناتجة لتطور المادة لن يكون لها طابع عام وستكون محددة للتماثل العالي الوشيك للنموذج الحالي. رياضياً، ترتبط هذه الخصوصية بحقيقة أنه بالنسبة للهندسة الفضائية المتجانسة التي تمت مناقشتها هنا، فإن مكونات موتر Ricci
هي أصفار متطابقة، وبالتالي فإن معادلات أينشتاين لن تسمح بحركة المادة (التي تعطي إجهادًا غير صفريًا لمكونات موتر الطاقة والزخم
). بمعنى آخر، يجب أن يكون الإطار المتزامن أيضًا متحركًا بشكل مشترك فيما يتعلق بالمادة. إذا كان أحد البدائل في eq. 19 u α = 0، u 0 = 1، يصبح ε ~ ( abc ) −4/3 ~ t −4/3 . يتم تجنب هذه الصعوبة إذا قام المرء بتضمين المصطلحات الرئيسية للمقياس المحدد (عند t → 0) فقط في النموذج وكتب فيه مسألة بتوزيع أولي تعسفي للكثافات والسرعات. ثم يتم تحديد مسار تطور المادة من خلال قوانينها العامة للحركة eq. 17 eq. 18 ينتج عنه eq. 21 . خلال كل حقبة كاسنر، تزداد الكثافة حسب القانون
-
(eq. 40)
حيث p 3، على النحو الوارد أعلاه، أكبر الأعداد ص 1، ص 2، ص 3 . تزداد كثافة المادة بشكل رتيب خلال كل تطور نحو التفرد.
تطور متري
تتوافق قيم u الكبيرة جدًا مع قوى كاسنر
-
(eq. 43)
التي هي قريبة من القيم (0، 0، 1). قيمتان قريبتان من الصفر، قريبتان أيضًا من بعضهما البعض، وبالتالي فإن التغييرات في نوعين من الأنواع الثلاثة "للاضطرابات" (المصطلحات مع λ و μ و في الجوانب اليمنى من eq. 26 ) هي أيضا متشابهة جدا. إذا كانت هذه المصطلحات في بداية مثل هذا العصر الطويل قريبة جدًا من القيم المطلقة في لحظة الانتقال بين حقبتين من عهود كاسنر (أو تم إجراؤها بشكل مصطنع من خلال تعيين الشروط الأولية)، فستظل قريبة خلال الجزء الأكبر من طول الحقبة. في هذه الحالة (وتسمى حالة التذبذبات الصغيرة)، يصبح التحليل القائم على عمل نوع واحد من الاضطرابات غير صحيح ؛ يجب على المرء أن يأخذ في الاعتبار التأثير المتزامن لنوعين من الاضطراب.
اثنان من الاضطرابات
ضع في اعتبارك حقبة طويلة، حيث خضعت اثنتان من الوظائف أ، ب، ج (فليكن أ و ب ) لتذبذبات صغيرة بينما تتناقص الوظيفة الثالثة (ج ) بشكل رتيب. سرعان ما تصبح الوظيفة الأخيرة صغيرة ؛ ضع في اعتبارك الحل فقط في المنطقة حيث يمكن للمرء أن يتجاهل c مقارنةً بـ a و b . يتم إجراء الحسابات أولاً للنموذج الفضائي من النوع IX عن طريق الاستبدال وفقًا لذلك λ = μ = ν = 1.[43]
بعد تجاهل الوظيفة c، فإن المعادلتين eq. 26 إعطاء
-
(eq. 44)
-
(eq. 45)
eq. 28 كمعادلة ثالثة، والتي تأخذ الشكل
-
(eq. 46)
حل eq. 44 مكتوب في النموذج
حيث α 0، ξ 0 هي ثوابت موجبة، و 0 هي الحد الأعلى لعصر المتغير τ. من الملائم تقديم متغير جديد (بدلاً من τ)
-
(eq. 47)
ثم
-
(eq. 48)
المعادلات eq. 45 eq. 46 يتم تحويلها عن طريق إدخال المتغير χ = α - β:
-
(eq. 49)
-
(eq. 50)
انخفاض τ من τ 0 إلى −∞ يتوافق مع انخفاض ξ من ξ 0 إلى 0. يتم الحصول على العصر الطويل مع إغلاق a و b (أي مع صغير)، المدروس هنا، إذا كانت ξ 0 كمية كبيرة جدًا. في الواقع، بشكل عام، حل eq. 49 في أول تقدير تقريبي بمقدار 1 / هو
-
(eq. 51)
حيث A ثابت ؛ المضاعف
يجعل χ كمية صغيرة بحيث يمكن استبدالها eq. 49 بواسطة sh 2χ ≈ 2χ. [note 13]
من eq. 50 واحد يحصل
بعد تحديد α و من eq. 48 eq. 51 وتوسيع ه α و β الإلكترونية في سلسلة وفقا لتقريب أعلاه، واحد يحصل أخيرا: [note 14]
-
(eq. 52)
-
(eq. 53)
يتم الحصول على العلاقة بين المتغير ξ والوقت t من خلال تكامل التعريف dt = abc d τ الذي يعطي
-
(eq. 54)
يجب أن يكون الثابت c 0 (قيمة с عند ξ = ξ 0 ) الآن c 0
α 0 ·
دعونا ننظر الآن في المجال ξ 1. هنا المصطلحات الرئيسية في حل eq. 49 هم:
حيث k ثابت في النطاق - 1 < ك <1 ؛ يضمن هذا الشرط أن المصطلح الأخير في eq. 49 صغير (يحتوي sh 2χ على ξ 2 ك و ξ −2 ك ). ثم، بعد تحديد α و و t، يحصل المرء على
-
(eq. 55)
هذا مرة أخرى هو وضع كاسنر مع وجود قوة t السالبة في الوظيفة c ( t ). [note 15]
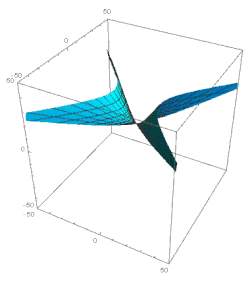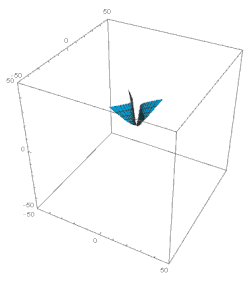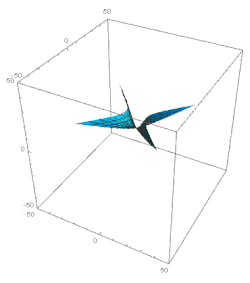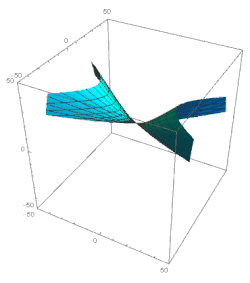
هذه النتائج تصور تطورًا مشابهًا نوعيًا لذلك الموصوف أعلاه. خلال فترة زمنية طويلة تتوافق مع قيمة ξ متناقصة كبيرة، تتأرجح الوظيفتان a و b، وتبقى قريبة من حيث الحجم ؛ في نفس الوقت، كلتا الوظيفتين أ و ب ببطء ( ) ينقص. فترة التذبذب ثابتة بالمتغير ξ : Δξ = 2π (أو، وهي نفسها، مع فترة ثابتة حسب الوقت اللوغاريتمي: Δ ln t = 2π Α 2 ). الوظيفة الثالثة، c، تتناقص بشكل رتيب بقانون قريب من c = c 0 t / t 0 .
يستمر هذا التطور حتى ξ ≈1 والصيغ eq. 52 eq. 53 لم تعد قابلة للتطبيق. تقابل مدتها الزمنية تغيير t من t 0 إلى القيمة t 1، المرتبطة بـ ξ 0 وفقًا لـ
-
(eq. 56)
يمكن تقديم العلاقة بين ξ و t خلال هذا الوقت في النموذج
-
(eq. 57)
بعد ذلك، كما رأينا من eq. 55، تبدأ دالة التناقص c في الزيادة بينما تبدأ الدالتان a و b في الانخفاض. تستمر حقبة كاسنر هذه حتى الشروط ج 2 / أ 2 ب 2 في eq. 22 يصبح eq. 22 ~ t 2 وتبدأ سلسلة التذبذبات التالية. يتم الحصول على قانون تغيير الكثافة خلال الحقبة الطويلة قيد المناقشة عن طريق استبدال eq. 52 في eq. 20 :
-
(eq. 58)
عندما تتغير من ξ 0 إلى ξ ≈1، تزداد الكثافة
مرات. يجب التأكيد على أنه على الرغم من أن الوظيفة c ( t ) تتغير بواسطة قانون، بالقرب من c ~ t، فإن المقياس المتري eq. 52 لا يتوافق مع مقياس كاسنر بقوى (0، 0، 1). الأخير يتوافق مع الحل الدقيق الذي وجده Taub [47] والذي يسمح به المعادلات. 26 - 27 وفي أي
-
(eq. 59)
حيث p، δ 1، δ 2 ثابتة. في المنطقة المقاربة τ → −∞، يمكن للمرء الحصول من هنا a = b = مقدار ثابت، c = مقدار ثابت. ر بعد الاستبدال е рτ = t . في هذا المقياس، تكون التفرد عند t = 0 غير مادية.
دعونا الآن نصف الدراسة المماثلة لنموذج النوع الثامن، مع استبدال المعادلات. eqs. 26 - 28 λ = -1، μ = ν = 1.[44] إذا خلال حقبة طويلة، وظيفة خفض مفردة النغمة هي، لا شيء يتغير في التحليل السابق: تجاهل 2 على الجانب الأيمن من المعادلات 26 و 28، ويعود إلى نفس المعادلات 49 و 50 (مع تدوين تغير). ومع ذلك، تحدث بعض التغييرات إذا كانت الوظيفة المتناقصة بشكل رتيب هي b أو c ؛ فليكن c. كما كان من قبل، لدى المرء معادلة 49 بنفس الرموز، وبالتالي، التعابير السابقة eq. 52 للوظائف a (ξ) و b (ξ)، ولكن تم استبدال 50
-
(eq. 60)
يصبح المصطلح الرئيسي بشكل عام ξ الآن
لذلك
-
(eq. 61)
قيمة c كدالة للوقت t مرة أخرى c = c 0 t / t 0 لكن اعتماد الوقت على ξ يتغير. يعتمد طول الحقبة الطويلة على ξ 0 وفقًا لـ
-
(eq. 62)
من ناحية أخرى، تحدد القيمة ξ 0 عدد التذبذبات للوظائف a و b خلال حقبة (تساوي ξ 0 / 2π). بالنظر إلى طول العصر في الوقت اللوغاريتمي (أي مع النسبة المعطاة t 0 / t 1 )، سيكون عدد التذبذبات للنوع الثامن، بشكل عام، أقل من النوع IX. بالنسبة لفترة التذبذبات، نحصل الآن على Δ ln t = πξ / 2 ؛ على عكس النوع التاسع، فإن الفترة ليست ثابتة طوال العصر الطويل، وتتناقص ببطء مع ξ.
مجال الوقت الصغير
تنتهك العصور الطويلة المسار "المنتظم" للتطور مما يجعل من الصعب دراسة تطور الفترات الزمنية التي تمتد عبر عدة عصور. ومع ذلك، يمكن إثبات أن مثل هذه الحالات "غير الطبيعية" تظهر في التطور التلقائي للنموذج إلى نقطة مفردة في الأوقات الصغيرة المتقاربة t على مسافات كبيرة بما يكفي من نقطة البداية ذات الظروف الأولية التعسفية. حتى في العصور الطويلة، تظل كلتا الوظيفتين المتذبذبتين أثناء التحولات بين عهود كاسنر مختلفة تمامًا لدرجة أن الانتقال يحدث تحت تأثير اضطراب واحد فقط. جميع النتائج في هذا القسم تتعلق بنفس القدر بنماذج من النوعين الثامن والتاسع.[48]
خلال كل حقبة كاسنر abc = Λ t، أي α + β + γ = ln Λ + ln t . عند التغيير من حقبة واحدة (بقيمة معينة للمعامل u ) إلى الحقبة التالية، يتم ضرب الثابت Λ بـ 1 + 2 p 1 = (1 - u + u 2 ) / (1 + u + u 2 ) < 1. وبالتالي يحدث انخفاض منهجي في. لكن من الضروري أن تكون القيمة المتوسطة (فيما يتعلق بأطوال k للعصور) للتغير الكامل لـ ln خلال حقبة ما محدودة. في الواقع، يمكن أن يكون الاختلاف في متوسط القيمة ناتجًا فقط عن زيادة سريعة جدًا في هذا التباين مع زيادة k . للحصول على قيمة كبيرة للمعامل u، ln (1 + 2 p 1 ) ≈ −2 / u . بالنسبة إلى k كبير، تكون القيمة القصوى u (max) = k + x ≈ k. ومن ثم فإن الاختلاف الكامل لـ ln Λ خلال حقبة ما يتم الحصول عليه من خلال مجموع النموذج
فقط مع المصطلحات التي تتوافق مع القيم الكبيرة لـ u مكتوبة. عندما يزيد k، يزداد هذا المجموع بمقدار ln k . لكن احتمالية ظهور حقبة ذات طول كبير k تقل بمقدار 1 / k 2 وفقًا لـ eq. 76 ؛ ومن ثم فإن القيمة المتوسطة للمبلغ أعلاه محدودة. وبالتالي، فإن الاختلاف المنهجي للكمية ln Λ على مدى عدد كبير من العصور سيكون متناسبًا مع هذا الرقم. ولكن يتم رؤيته في eq. 85 أنه مع t → 0، يزيد الرقم s فقط مثل ln | ln t |. وبالتالي في الحد المقارب لـ t صغير بشكل تعسفي، يمكن بالفعل إهمال المصطلح ln Λ بالمقارنة مع ln t . في هذا التقريب [note 16]
-
(eq. 63)
حيث Ω تشير إلى "الوقت اللوغاريتمي"
-
(eq. 64)
ويمكن اعتبار عملية تحولات الحقبة على أنها سلسلة من الومضات الزمنية القصيرة. تخضع مقادير الحد الأقصى لوظائف المقياس المتذبذب أيضًا لتغير منهجي. من eq. 39 أجل u ≫ 1 يتبع ذلك
. بالطريقة نفسها التي تم إجراؤها أعلاه للكمية ln Λ، يمكن للمرء بالتالي أن يستنتج أن متوسط الانخفاض في ارتفاع الحد الأقصى خلال حقبة ما محدود وأن الانخفاض الكلي على مدى عدد كبير من العصور يزداد مع t → 0 فقط مثل ln Ω. في الوقت نفسه، يتم تخفيض الحد الأدنى، وبنفس الطريقة، زيادة سعة التذبذبات، ( eq. 77 ) بما يتناسب مع Ω. بالتوافق مع التقريب المعتمد، يتم إهمال خفض الحد الأقصى بالمقارنة مع زيادة السعات بحيث تكون α max = 0، β max = 0، γ max = 0 للقيم القصوى لجميع الوظائف المتذبذبة والكميات α،، γ قم بتشغيل فقط من خلال القيم السالبة التي ترتبط ببعضها البعض في كل لحظة من الوقت بواسطة العلاقة eq. 63 .

بالنظر إلى مثل هذا التغيير الفوري للعصور، يتم تجاهل الفترات الانتقالية على أنها صغيرة مقارنة بطول الحقبة ؛ تم استيفاء هذا الشرط في الواقع. [note 17] يتطلب استبدال α و β و الحد الأقصى بأصفار أن تكون الكميات ln (| p 1 | Λ) صغيرة بالمقارنة مع اتساع تذبذبات الوظائف المعنية. كما ذكر أعلاه، أثناء الانتقال بين العصور | ص 1 | يمكن أن تصبح القيم صغيرة جدًا بينما لا يرتبط حجمها واحتمال حدوثها بمدى التذبذب في اللحظة المعنية. لذلك، من حيث المبدأ، من الممكن الوصول إلى هذا الحجم الصغير | ص 1 | القيم التي تم انتهاك الشرط أعلاه (صفر حد أقصى). يمكن أن يؤدي هذا الانخفاض الحاد في α max إلى مواقف خاصة مختلفة يكون فيها الانتقال بين فترات كاسنر بواسطة القاعدة eq. 37 غير صحيح (بما في ذلك الحالات المذكورة أعلاه ). هذه المواقف "الخطيرة" يمكن أن تخرق القوانين المستخدمة في التحليل الإحصائي أدناه. ومع ذلك، وكما ذكرنا، فإن احتمال مثل هذه الانحرافات يتقارب بشكل مقارب إلى الصفر ؛ سيتم مناقشة هذه المسألة أدناه.
ضع في اعتبارك حقبة تحتوي على فترات k كاسنر مع وجود معلمة u تعمل عبر القيم
-
(eq. 65)
ولنفترض أن α و هما الوظيفتان المتذبذبتان خلال هذا العصر (الشكل 4). [note 18] اللحظات الأولية لفترات كاسنر ذات المعلمات u n هي n . في كل لحظة أولية، تكون إحدى القيمتين α أو صفرًا، بينما تحتوي الأخرى على حد أدنى. القيم α أو في الحدود الدنيا المتتالية، أي في اللحظات n
-
(eq. 66)
(لا يميز الحدود الدنيا α و β). يمكن للقيم δ n التي تقيس تلك الحدود الدنيا في وحدات n ذات الصلة أن تعمل بين 0 و 1. الوظيفة γ تتناقص بشكل رتيب خلال هذا العصر ؛ حسب eq. 63 قيمتها باللحظة Ω n هي
-
(eq. 67)
خلال الحقبة التي تبدأ من اللحظة Ω n وتنتهي في اللحظة Ω n +1 تزيد إحدى الوظائف α أو β من −δ n Ω n إلى الصفر بينما تقل الأخرى من 0 إلى −δ n +1 Ω n +1 بالخطي القوانين، على التوالي:
- و
- مما أدى إلى علاقة التكرار
-
(eq. 68)
وطول العصر اللوغاريتمي
-
(eq. 69)
حيث، باختصار، f ( u ) = 1 + u + u 2 . يتم الحصول على مجموع أطوال الحقبة n بواسطة الصيغة
-
(eq. 70)
يمكن رؤيته من eq. 68 أن | α n + 1 | > | α n |، أي، تزداد اتساع التذبذب للوظائف α و خلال العصر بأكمله على الرغم من أن العوامل δ n قد تكون صغيرة. إذا كان الحد الأدنى في بداية العصر عميقًا، فلن يصبح الحد الأدنى التالي أقل ضحالة ؛ بمعنى آخر، البقايا | α - β | في لحظة الانتقال بين عهود كاسنر لا تزال كبيرة. لا يعتمد هذا التأكيد على طول العصر k لأن الانتقالات بين العصور يتم تحديدها من خلال القاعدة المشتركة eq. 37 أيضا لعصور طويلة.
سعة التذبذب الأخيرة للوظائف α أو في عصر معين مرتبطة بسعة التذبذب الأول بالعلاقة | α k −1 | = | α 0 | ( ك + س ) / (1 + س ). حتى في ك الصورة صغيرة مثل عدة وحدات س يمكن تجاهلها في المقارنة إلى k بحيث زيادة α وسعة التذبذب بيتا تصبح متناسبة مع طول الحقبة. لوظائف 'وه' = α و ب ه = β يعني ذلك أنه إذا كانت السعة من التذبذبات في بداية عصر كان A 0، في نهاية هذا العصر السعة ستصبح .
كما يزداد طول فترات كاسنر (في الوقت اللوغاريتمي) داخل عصر معين ؛ من السهل حساب من eq. 69 أن Δ ن +1 > Δ ن . [note 19] الطول الإجمالي للعصر هو
-
(eq. 71)
(المصطلح مع 1 / x ينشأ من الحقبة الأخيرة، k -th، التي يكون طولها كبيرًا عند x الصغيرة ؛ راجع. الصورة 2). لحظة Ω ن عندما ك -th الحقبة من نهايات عصر معين هو في نفس الوقت لحظة Ω '0 من بداية الحقبة المقبلة. في حقبة كاسنر الأولى من العصر الجديد، كانت الدالة γ هي الأولى التي ارتفعت من أدنى قيمة γ ك = - Ω ك (1 - δ ك ) التي وصلت إليها في العصر السابق ؛ تلعب هذه القيمة دور سعة البداية δ ' 0 Ω' 0 لسلسلة التذبذبات الجديدة. من السهل الحصول على ما يلي:
-
(eq. 72)
من الواضح أن δ ' 0 Ω' 0 > 0 Ω 0 . حتى في ك يست كبيرة جدا في زيادة السعة مهمة جدا: وظيفة ج = ه γ يبدأ ذبذبة من السعة
. يتم ترك المسألة المتعلقة بالحالات "الخطيرة" المذكورة أعلاه من الانخفاض الحاد في حد التذبذب العلوي جانبًا في الوقت الحالي.
حسب eq. 40 الزيادة في كثافة المادة خلال العهود الأولى (ك - 1) تعطى بواسطة الصيغة
حتى آخر k لعصر معين، في u = x <1 أعظم قوة هو P 2 (x) (لا P 3 (x)). لذلك، من أجل زيادة الكثافة خلال العصر بأكمله، يحصل المرء
-
(eq. 73)
لذلك، حتى مع عدم وجود قيم k كبيرة جدًا،
. خلال العصر التالي (بطول k ') ستزداد الكثافة بشكل أسرع بسبب زيادة سعة البداية A 0 ':
، إلخ. توضح هذه الصيغ الزيادة الحادة في كثافة المادة.
التحليل الإحصائي قرب التفرد
يكتسب تسلسل أطوال الحقبة k ( s )، المقاسة بعدد فترات كاسنر الموجودة فيها، طابع عملية عشوائية مقاربًا. الأمر نفسه يتعلق أيضًا بتسلسل تقاطعات أزواج الوظائف المتذبذبة عند الانتقال من عصر إلى آخر (يعتمد ذلك على ما إذا كانت الأرقام k ( s ) زوجية أو فردية). مصدر هذه العشوائية هو eqs. 41 - 42 التي بموجبها يتم تحديد الانتقال من عصر إلى آخر في تسلسل عدد لا نهائي من قيم u. تنص هذه القاعدة، بعبارة أخرى، على أنه إذا بدأ التسلسل اللانهائي بأكمله بقيمة أولية معينة
، ثم أطوال العصور ك (0)، ك (1)، ...، هي الأرقام في توسيع الكسر المستمر.
-
(eq. 73a)
يتوافق هذا التوسيع مع تحويل الفاصل الزمني [0، 1] إلى نفسه بواسطة الصيغة Tx = {1 / x }، أي x s +1 = {1 / x s }. ينتمي هذا التحول إلى ما يسمى بتحولات التوسع للفاصل الزمني [0، 1]، أي التحويلات x → f ( x ) مع | و ′ ( س ) | > 1. تمتلك هذه التحولات خاصية عدم الاستقرار الأسي: إذا أخذنا في البداية نقطتين قريبتين، فإن المسافة المتبادلة بينهما تزداد بشكل كبير في ظل تكرارات التحولات. من المعروف أن عدم الاستقرار الأسي يؤدي إلى ظهور خصائص عشوائية قوية.
من الممكن التحول إلى وصف احتمالي لمثل هذا التسلسل من خلال عدم مراعاة قيمة أولية محددة x (0) ولكن القيم x (0) = x الموزعة في الفترة من 0 إلى 1 وفقًا لقانون توزيع احتمالي معين ث 0 ( x ). ثم قيم x (s) التي تنتهي كل عصر سيكون لها أيضًا توزيعات تتبع قوانين معينة w s (x) . لنفترض أن w s (x) dx هو احتمال أن ينتهي العصر s بالقيمة الكذب في فترة زمنية محددة dx .
قيمة X (s) = X، والتي تنتهي في ليالي عصر s-th، يمكن أن تنجم عن الأولي (لهذا العصر) القيم ، حيث ك = 1، 2، ... ؛ هذه القيم تتوافق مع القيم x ( s –1) = 1 / ( k + x ) للعصر السابق. مع ملاحظة ذلك، يمكن للمرء أن يكتب علاقة التكرار التالية، والتي تعبر عن توزيع الاحتمالات w s (x) من حيث التوزيع w s –1 ( x ):
حيث λ a، μ a، s 1، s 2 هي وظائف تعسفية لجميع الإحداثيات الثلاثة x، y، z، المرتبطة بشروط أخرى
-
(eq. 73c)
إذا كان التوزيع w s ( x ) يميل إلى زيادة s إلى توزيع محدد ثابت (مستقل عن s ) w ( x )، فيجب أن يفي الأخير بمعادلة تم الحصول عليها من eq. 73c بإسقاط مؤشرات الدوالين w s −1 ( x ) و w s ( x ). هذه المعادلة لها حل
-
(eq. 74)
(تم تطبيعه إلى الوحدة ويؤخذ إلى الدرجة الأولى من x ). [note 20] من أجل أن يكون للعصر s طولًا k، يجب أن ينتهي العصر السابق برقم x في الفاصل الزمني بين 1 / ( k + 1) و 1 / k . لذلك، فإن احتمال أن يكون للعصر طول ك يساوي (في الحد الثابت)
-
(eq. 75)
عند قيم كبيرة لـ k
-
(eq. 76)
في ربط الخصائص الإحصائية للنموذج الكوني مع ارجوديك خصائص التحول س ق +1 = {1 / س ق} يجب ذكر نقطة مهمة. في تسلسل لا نهائي من الأرقام x التي تم إنشاؤها وفقًا لهذه القاعدة، ستتم ملاحظة قيم x الصغيرة (ولكن لا تتلاشى أبدًا) بشكل تعسفي مقابل أطوال كبيرة بشكل تعسفي k. يمكن لمثل هذه الحالات (بأي حال من الأحوال بالضرورة!) أن تؤدي إلى بعض المواقف المحددة عندما تتبادل فكرة العصور، كما هو الحال في تسلسل عهود كاسنر، بعضها البعض وفقًا للقاعدة eq. 37، يفقد معناه (على الرغم من أن الوضع التذبذب لتطور النموذج لا يزال قائماً). يمكن أن يتجلى مثل هذا الوضع "الشاذ"، على سبيل المثال، في ضرورة الاحتفاظ بالجانب الأيمن من eq. 26 مصطلحًا ليس فقط مع إحدى الوظائف أ، ب، ج (على سبيل المثال، أ 4 )، كما هو الحال في التبادل "العادي" لعصر كاسنر، ولكن في نفس الوقت مع اثنين منهم (على سبيل المثال، أ 4، ب 4، أ 2 ب 2 ).
عند الخروج من سلسلة "شاذة" من التذبذبات، يتم استعادة سلسلة من العصور المنتظمة. التحليل الإحصائي لسلوك النموذج الذي يعتمد بالكامل على التكرارات المنتظمة للتحولات eq. 42 من خلال نظرية مهمة: يميل احتمال ظهور الحالات الشاذة بشكل مقارب إلى الصفر حيث أن عدد التكرارات s → ∞ (أي الوقت t → 0) الذي تم إثباته في نهاية هذا القسم. تعود صحة هذا التأكيد إلى حد كبير إلى المعدل السريع جدًا للزيادة في اتساع التذبذب خلال كل عصر وخاصة في الانتقال من عصر إلى آخر.
إن عملية استرخاء النموذج الكوني إلى النظام الإحصائي "الثابت" (مع بدء t → 0 من "لحظة أولية" معينة) أقل إثارة للاهتمام، مع ذلك، من خصائص هذا النظام نفسه مع أخذ الاعتبار الواجب للخرسانة. قوانين تغير الخصائص الفيزيائية للنموذج خلال العصور المتعاقبة.
يتم الحصول على فكرة عن المعدل الذي يتم به تعيين التوزيع الثابت من المثال التالي. دع القيم الأولية x (0) توزع في فاصل زمني ضيق للعرض δ x (0) حول بعض الأرقام المحددة. eq. 73c علاقة التكرار. eq. 73c (أو مباشرة من التوسع eq. 73a ) من السهل استنتاج أن عروض التوزيعات w s ( x ) (حول أرقام محددة أخرى) ستكون عندئذٍ مساوية لـ
-
(eq. 76a)
(هذا التعبير صالح فقط طالما أنه يحدد الكميات δ x (s) 1).
القيمة المتوسطة ، المحسوبة من هذا التوزيع، تتباعد لوغاريتميًا. للحصول على تسلسل، مقطوع عند عدد كبير جدًا، ولكنه لا يزال محدودًا، N، واحد لديه . فائدة المتوسط في هذه الحالة محدودة للغاية بسبب عدم استقراره: بسبب الانخفاض البطيء لـ W ( k )، تتباعد التقلبات في k أسرع من متوسطها. السمة الأكثر ملاءمة لهذا التسلسل هي احتمال أن ينتمي الرقم المختار عشوائيًا منه إلى عصر بطول K حيث يكون K كبيرًا. هذا الاحتمال هو ln K / ln N. إنه صغير إذا . في هذا الصدد، يمكن للمرء أن يقول إن رقمًا تم اختياره عشوائيًا من تسلسل معين ينتمي إلى عصر طويل مع احتمال كبير.
من الملائم متوسط التعبيرات التي تعتمد في وقت واحد على k ( s ) و x ( s ) . نظرًا لأن هذه الكميات مشتقة من نفس الكمية x ( s –1) (التي تنتهي العصر السابق)، وفقًا للصيغة k ( s ) + x ( s ) = 1 / x ( s –1)، فإن إحصائهما لا يمكن اعتبار التوزيعات مستقلة. يمكن الحصول على التوزيع المشترك W s ( k، x ) dx لكلا الكميتين من التوزيع w s –1 ( x ) dx من خلال إجراء الاستبدال في الأخير x → 1 / ( x + k ). بمعنى آخر، يتم إعطاء الدالة W s ( k، x ) من خلال التعبير ذاته الموجود أسفل علامة الجمع في الجانب الأيمن من eq. 73c . في الحد الثابت، مع أخذ w من eq. 74، يتم الحصول على
-
(eq. 76b)
جمع هذا التوزيع على k يعيدنا إلى eq. 74، والتكامل فيما يتعلق dx إلى eq. 75.
الصيغ المتكررة تحديد الانتقالات بين العصور هي إعادة مكتوبة مع مؤشر الصورة ترقيم العصور المتعاقبة (وليس العهود كاسنر في حقبة معينة!)، ابتداء من عصر بعض (ق = 0) تعرف بأنها الأولي. Ω ( s ) و ε ( s ) هي، على التوالي، اللحظة الأولية وكثافة المادة الأولية في العصر s ؛ δ ( s ) Ω ( s ) هي سعة التذبذب الأولية لهذا الزوج من الوظائف α، β،، والتي تتأرجح في عصر معين: k ( s ) هو طول العصر s، و x ( s ) يحدد طول (عدد عهود كاسنر) للعصر التالي وفقًا لـ k ( s +1) = [1 / x ( s ) ]. وفقًا لـ eqs. 71 - 73.
-
(eq. 77)
-
(eq. 78)
-
(eq. 79)
تم تقديم (ξ ( s ) في eq. 77 لاستخدامها لاحقًا).
الكميات δ ( s ) لها توزيع إحصائي ثابت ثابت P (δ) ومستقرة (تقلبات نسبية صغيرة) تعني القيمة. لتحديدها، [48] (مع التحفظات اللازمة) طريقة تقريبية تعتمد على افتراض الاستقلال الإحصائي للكمية العشوائية δ ( s ) والكميات العشوائية k ( s )، x ( s ) . بالنسبة للوظيفة P (δ)، تم إعداد معادلة متكاملة تعبر عن حقيقة أن الكميات δ ( s +1) و δ ( s ) مترابطة بواسطة العلاقة eq. 78 لها نفس التوزيع ؛ تم حل هذه المعادلة عدديا. في عمل لاحق، لخلاتنيكوف.[49] حيث أظهر أن التوزيع P (δ) يمكن إيجاده بالضبط بطريقة تحليلية.
بالنسبة للخصائص الإحصائية في الحد الثابت، من المعقول إدخال ما يسمى بالامتداد الطبيعي للتحول Tx = {1 / x } من خلال استمراره دون حدود للمؤشرات السالبة. بخلاف ذلك، يعد هذا انتقالًا من تسلسل لا نهائي من جانب واحد للأرقام ( x 0، x 1، x 2، ...)، متصلة بواسطة المساواة Tx = {1 / x }، إلى "مضاعف لانهائي" تسلسل X = (...، x −1، x 0، x 1، x 2، ...) للأرقام المتصلة بنفس المساواة لجميع –∞ < s <. بالطبع، هذا التوسع ليس فريدًا من نوعه في المعنى الحرفي للكلمة (نظرًا لأن x s –1 لا يتم تحديده بشكل فريد بواسطة x s )، ولكن جميع الخصائص الإحصائية للتسلسل الممتد موحدة على طولها بالكامل، أي أنها ثابتة مع فيما يتعلق بالنقل التعسفي (و x 0 يفقد معناه لشرط "أولي"). التسلسل X يكافئ سلسلة من الأعداد الصحيحة K = (...، k −1، k 0، k 1، k 2، ...)، التي تم إنشاؤها بواسطة القاعدة k s = [1 / x s –1 ] . عكسيًا، يتم تحديد كل عدد من X بواسطة الأعداد الصحيحة لـ K ككسر مستمر لانهائي.
-
(eq. 79a)
(راحة إدخال الترميز
مع تحويل الفهرس بمقدار 1 سيصبح واضحًا في ما يلي). للتدوين المختصر، يُشار إلى الكسر المستمر ببساطة عن طريق تعداد قواسمه (بين قوسين معقوفين) ؛ ثم تعريف
يمكن كتابتها كـ
-
(eq. 79b)
يتم تحديد الكميات العكسية بواسطة كسر مستمر مع تسلسل إلى الوراء (في اتجاه المؤشرات المتناقصة) من القواسم
-
(eq. 79c)
eq. 78 علاقة التكرار. eq. 78 عن طريق إدخال التدوين η s = (1 - δ s ) / δ s مؤقتًا. ثم eq. 78 يمكن إعادة كتابة eq. 78
عن طريق التكرار يتم الحصول على جزء مستمر لانهائي
لذلك
وأخيرا
-
(eq. 79d)
يحتوي هذا التعبير لδ الصورة اثنين فقط (بدلا من ثلاثة في [48] ) كميات عشوائية
و
، يفترض كل منها قيمًا في الفترة [0، 1]. يتبع من تعريف eq. 79c ذلك
. ومن ثم فإن تحول التسلسل X بأكمله بخطوة واحدة إلى اليمين يعني تحولًا مشتركًا للكميات
و
وفق
-
(eq. 79e)
هذا تعيين واحد لواحد في مربع الوحدة . وبالتالي لدينا الآن تحويل واحد إلى واحد لكميتين بدلاً من تحويل ليس واحد إلى واحد Tx = {1 / x } لكمية واحدة. الكميات
و
لها توزيع ثابت مشترك P ( x +، x - ). منذ eq. 79e عبارة عن تحويل واحد إلى واحد، ويتم التعبير عن شرط أن يكون التوزيع ثابتًا ببساطة بواسطة معادلة دالة
-
(eq. 79f)
حيث J هو جاكوبي من التحول.
يؤدي تغيير التسلسل X بخطوة واحدة إلى التحول التالي T لمربع الوحدة:
(مع و ، راجع. eq. 79e ). تحدد الكثافة P ( x، y ) المقياس الثابت لهذا التحول. من الطبيعي أن نفترض أن P ( x، y ) دالة متماثلة لـ x و y . هذا يعني أن المقياس ثابت فيما يتعلق بالتحول S ( x، y ) = ( y، x ) وبالتالي فيما يتعلق بالمنتج ST مع ST ( x، y ) = ( x ″، y ″ )،
من الواضح أن ST لديها أول متكامل H = 1 / x + y . على السطر H = const ≡ c، يكون للتحويل الشكل
ومن ثم يجب أن تكون كثافة القياس الثابتة لـ ST من الشكل
عند حساب التناظر P ( x، y ) = P ( y، x )، يصبح هذا f ( c ) = c −2 وبالتالي (بعد التطبيع)
-
(eq. 79g)
(تكامله على x + أو x - ينتج عنه الدالة w ( x ) eq. 74 ). تم استخدام تقليل التحول إلى رسم الخرائط واحد لواحد بالفعل بواسطة تشيرنوف وبارو [50] وحصلوا على صيغة على شكل eq. 79g لكن للمتغيرات الأخرى ؛ ورقتهم لا تحتوي على تطبيقات للمشكلات التي تم النظر فيها في صيغة خلاتنيكوف.[49]
eq. 79g يتم التحقق منها أيضًا عن طريق الحساب المباشر؛ اليعقوبي من التحول eq. 79e هو
(في حسابه يجب على المرء أن يلاحظ ذلك ).

بواسطة eq. 79d δ s من حيث الكميات العشوائية x + و x -، تتيح معرفة التوزيع المشترك بينهما حساب التوزيع الإحصائي P (δ) من خلال دمج P ( x +، x - ) على أحد المتغيرات بقيمة ثابتة δ. بسبب تناظر وظيفة eq. 79g فيما يتعلق بالمتغيرات x + و x -، P () = P (1 - δ)، أي أن الوظيفة P (δ) متناظرة بالنسبة للنقطة δ = 1/2. ثم
عند تقييم هذا التكامل (لـ 0 δ ≤ 1/2 ثم الاستفادة من التناظر المذكور أعلاه)، أخيرًا
-
(eq. 79h)
القيمة المتوسطة = 1/2 بالفعل نتيجة لتماثل الوظيفة P (δ). وبالتالي، فإن القيمة المتوسطة للسعة الأولية (في كل عصر) للتذبذبات للوظائف α، β، تزداد مثل Ω / 2.
تم العثور على علاقة ذات دلالة إحصائية بين فترات زمنية كبيرة Ω وعدد من عصور الصورة الواردة فيها من خلال تطبيق المتكررة من eq. 77 :
-
(eq. 80)
ومع ذلك، فإن حساب المتوسط المباشر لهذه المعادلة لا معنى له: بسبب الانخفاض البطيء في الوظيفة W ( k ) eq. 76، فإن متوسط قيم كمية exp ( s ) غير مستقرة بالمعنى أعلاه - تزداد التقلبات بسرعة أكبر من متوسط القيمة نفسها مع زيادة منطقة المتوسط. يتم التخلص من عدم الاستقرار هذا بأخذ اللوغاريتم: الفاصل الزمني "اللوغاريتمي المزدوج"
-
(eq. 81)
يتم التعبير عنها بمجموع الكميات ξ ( p ) التي لها توزيع إحصائي ثابت. متوسط قيمة τ هو
. لكي يحسب
لاحظ أن eq. 77 يمكن إعادة كتابة eq. 77
-
(eq. 81a)
للتوزيع الثابت
وبفضل تناظر الوظيفة P (δ) أيضًا
. لذلك
(w ( x) من eq. 74)،
-
(eq. 82)
الذي يحدد وقت مضاعف لوغاريتمي يعني الفاصلة التي تحتوي على الصورة العصور المتعاقبة. للقيم والصور الكبيرة عدد من المصطلحات في eq. 81 كبير ووفقًا للنظريات العامة لنظرية إرغوديك، يتم توزيع قيم τ s حولها
وفقًا لقانون جاوس مع الكثافة
-
(eq. 82a)
يعد حساب التباين D τ أكثر تعقيدًا لأنه ليس فقط معرفة
و
هناك حاجة أيضا ولكن أيضا من الارتباطات
. يمكن تبسيط الحساب عن طريق إعادة ترتيب المصطلحات في مجموع eq. 81 . باستخدام eq. 81a يمكن إعادة كتابة المجموع كـ
لا يزيد المصطلحان الأخيران مع زيادة s ؛ هذه الشروط يمكن أن يتم حذف مثل القوانين التي تحد عن الصورة الكبيرة هي التي تسيطر. ثم
-
(eq. 82b)
( eq. 79d for p في الاعتبار). إلى نفس الدقة (أي حتى الشروط التي لا تزيد مع ق ) المساواة
-
(eq. 82c)
وبالتالي
من خلال جمع هذه الهوية على p eq. 82c تم الحصول على eq. 82c أخيرًا مرة أخرى بنفس الدقة
تم تغييره لـ x p تحت علامة الجمع وبالتالي يمثل τ s كـ
-
(eq. 83)
تباين هذا المجموع في حدود s الكبيرة هو
-
خطأ رياضيات (خطأ في الصياغة): {\displaystyle D_{{ au}_s} = \overline{ \left ( au_s - \overline{ au_s} ight )^2} pprox s \left \{ \overline{\eta^2} - ar{\eta}^2 + 2 \sum_{p=1}^{\infty} \left ( \overline{\eta_0 \eta_p} - ar{\eta}^2 ight ) ight \}}
(eq. 84)
يؤخذ في الاعتبار أنه بحكم التجانس الإحصائي للتسلسل X فإن الارتباطات
تعتمد فقط على الاختلافات | ع - ع ′ القيمة المتوسطة
؛ المربع المتوسط
من خلال مراعاة قيم العلاقات المتبادلة مع p = 1، 2، 3 (محسوبة عدديًا) يتم الحصول على النتيجة النهائية D τ s = (3.5 ± 0.1) s .
إلى زيادة الصورة تذبذب نسبي
يميل إلى الصفر مثل s −1/2 . بمعنى آخر، العلاقة الإحصائية eq. 82 يصبح شبه مؤكد في الصورة الكبيرة. وهذا يجعل من الممكن عكس العلاقة، أي لتمثيل أنها اعتماد متوسط عدد عصور الصورة τ التي يتم تبادلها في τ فترة معينة من الوقت لوغاريتمي مزدوج:
-
(eq. 85)
التوزيع الإحصائي للقيم الدقيقة لـ Sτ حول المتوسط هو أيضا التمويه مع الفرق والتباين
يتم إعطاء التوزيع الإحصائي المعني بنفس التوزيع الغوسي حيث يكون المتغير العشوائي الآن s τ عند معين τ:
-
(eq. 86)
من وجهة النظر هذه، فإن مصدر السلوك الإحصائي هو التعسف في اختيار نقطة البداية للفاصل τ المتراكب على التسلسل اللانهائي للعصور المتغيرة.
فيما يتعلق بكثافة المادة، eq. 79 يمكن إعادة كتابتها مع حساب eq. 80 في النموذج
وبعد ذلك، لتغيير إجمالي الطاقة خلال الصورة العصور،
-
(eq. 87)
المصطلح الذي يحتوي على مجموع بواسطة p يعطي المساهمة الرئيسية لهذا التعبير لأنه يحتوي على أس ذو قوة كبيرة. ترك هذا المصطلح فقط ومتوسط eq. 87، يحصل المرء على التعبير في جانبه الأيمن
الذي يتزامن مع eq. 82 ؛ جميع المصطلحات الأخرى في مجموع (أيضا حيث مع η ليالي في صلاحياتهم) تؤدي فقط إلى التصويبات من النظام النسبي 1 / ثانية. وبالتالي،
-
(eq. 88)
بحكم الطابع شبه المؤكد للعلاقة بين τ s و s eq. 88 يمكن كتابة eq. 88
الذي يحدد قيمة اللوغاريتم المزدوج لزيادة الكثافة التي تراوحت بحسب الفترات الزمنية المزدوج لوغاريتمي نظرا τ أو عدد معين من عصور الصورة.
توجد هذه العلاقات الإحصائية المستقرة خصيصًا للفترات الزمنية اللوغاريتمية المزدوجة ولزيادة الكثافة. بالنسبة للخصائص الأخرى، على سبيل المثال، ln (ε ( s ) / ε (0) ) أو Ω (s) / Ω (0) = exp s، يزداد التقلب النسبي أضعافًا مضاعفة مع زيادة نطاق المتوسط وبالتالي يتم إلغاء مصطلح متوسط القيمة ذات معنى ثابت.
أصل العلاقة الإحصائية eq. 88 بالفعل من القانون الأولي الذي يحكم تباين الكثافة خلال عهود كاسنر الفردية. حسب eq. 21، خلال التطور بأكمله لدينا
مع تغيير 1 - p 3 ( t ) من حقبة إلى أخرى، عبر القيم في الفاصل الزمني من 0 إلى 1. المصطلح ln Ω = ln ln (1 / t ) يزيد بشكل رتيب ؛ من ناحية أخرى، يمكن للمصطلح ln2 (1 - p 3 ) أن يفترض قيمًا كبيرة (يمكن مقارنتها بـ ln Ω) فقط عندما تظهر قيم p 3 قريبة جدًا من الوحدة (أي صغيرة جدًا | p 1 |). هذه هي بالتحديد الحالات "الخطيرة" التي تزعج المسار المنتظم للتطور الذي تعبر عنه العلاقات المتكررة eq. 77 - eq. 79 .
يبقى إظهار أن مثل هذه الحالات لا تنشأ في الواقع في نظام الحد المقارب. يبدأ التطور التلقائي للنموذج في لحظة معينة يتم فيها تحديد شروط أولية محددة بطريقة تعسفية. وبناءً على ذلك، فإن كلمة "مقارب" تعني نظامًا بعيدًا بدرجة كافية عن اللحظة الأولية المختارة.
الحالات الخطيرة هي تلك التي تظهر فيها قيم صغيرة جدًا للمعامل u = x (وبالتالي أيضًا | p 1 | ≈ x ) في نهاية العصر. معيار لاختيار مثل هذه الحالات هو عدم المساواة
أين | α ( s ) | هو عمق الدنيا الأولي من الوظائف التي ذبذبة في عصر الصورة (فإنه سيكون أكثر ملاءمة لاختيار السعة النهائية، ولكن هذا من شأنه أن يعزز فقط معيار الاختيار).
يتم تحديد قيمة x (0) في العصر الأول بالشروط الأولية. القيم الخطرة هي القيم الموجودة في الفاصل الزمني δ x (0) ~ exp (- | α (0) |)، وكذلك في الفواصل الزمنية التي يمكن أن تؤدي إلى حالات خطيرة في العصور التالية. من أجل أن تقع x ( s ) في الفترة الخطرة δ x ( s ) ~ exp (- | α ( s ) |)، يجب أن تكمن القيمة الأولية x (0) في فاصل عرض δ x (0) ~ δ x ( s ) / ك (1) ^ 2 ... ك ( ق ) ^ 2 . [45] لذلك، من وحدة الفاصل الزمني لجميع القيم الممكنة لـ x (0)، ستظهر الحالات الخطيرة في الأجزاء λ من هذه الفترة الزمنية:
(يتم أخذ المجموع الداخلي على جميع القيم k (1)، k (2)، ...، ك ( ق ) من 1 إلى ∞). من السهل إثبات أن هذا العصر يتقارب مع القيمة λ 1 الذي يتم تحديد ترتيب حجمه بواسطة المصطلح الأول في eq. 90 . يمكن إثبات ذلك من خلال التخصص القوي للعصر الذي يستبدل فيه المرء | α ( ق ) | = (ث + 1) | α (0) |، بغض النظر عن أطوال العصور k (1)، k (2)،. . . (في الواقع | α ( s ) | زيادة أسرع بكثير ؛ حتى في أكثر الحالات غير المواتية k (1) = k (2) = ... = 1 قيم | α ( s ) | زيادة مثل q s | α (0 ) | مع q > 1. ) مشيرا إلى ذلك
إذا كانت القيمة الأولية لـ x (0) تقع خارج المنطقة الخطرة، فلن تكون هناك حالات خطيرة. إذا كانت تقع داخل هذه المنطقة، تحدث حالات خطيرة، ولكن عند اكتمالها، يستأنف النموذج تطورًا "منتظمًا" بقيمة أولية جديدة والتي قد تأتي في بعض الأحيان فقط (مع احتمال λ) في الفترة الخطرة. تحدث الحالات الخطيرة المتكررة باحتمالات λ 2، λ 3، ...، تتقارب بشكل مقارب إلى الصفر.
حل عام مع الذبذبات الصغيرة
في النماذج المذكورة أعلاه، تمت دراسة التطور المتري بالقرب من التفرد على مثال مقاييس الفضاء المتجانسة. يتضح من خاصية هذا التطور أن البناء التحليلي للحل العام لتفرد من هذا النوع يجب أن يتم بشكل منفصل لكل من مكونات التطور الأساسية: لعصور كاسنر، من أجل عملية الانتقال بين العصور التي تسببها " الاضطرابات "، لفترات طويلة مع اضطرابين يعملان في وقت واحد. خلال حقبة كاسنر (أي عند الاضطرابات الصغيرة)، يتم إعطاء المقياس بواسطة eq. 7 بدون الشرط λ = 0.
طور تفرد بي كي إل أيضاً نموذجًا مستقلًا عن توزيع المادة (متجانس أو غير متجانس) لعصر طويل مع تذبذبات صغيرة. تبين أن الاعتماد على الوقت لهذا الحل مشابه جدًا لتلك الموجودة في الحالة الخاصة للنماذج المتجانسة ؛ يمكن الحصول على الأخير من نموذج التوزيع المستقل عن طريق اختيار خاص للوظائف التعسفية الواردة فيه.[51]
من الملائم، مع ذلك، بناء حل عام في نظام إحداثيات يختلف نوعًا ما عن الإطار المرجعي المتزامن: g 0α = 0 كما هو الحال في الإطار المتزامن، ولكن بدلاً من g 00 = 1 أصبح الآن g 00 = - g 33 . تحديد موتر الفراغ المترية γ αβ = - g αβ واحد، لذلك
-
(eq. 91)
يتم كتابة إحداثي الفضاء الخاص كـ x 3 = z ويتم كتابة إحداثي الوقت كـ x 0 = ξ (يختلف عن الوقت المناسب t ) ؛ سيظهر أن ξ يتوافق مع نفس المتغير المحدد في النماذج المتجانسة. يُشار إلى التفاضل بـ ξ و z، على التوالي، بالنقطة والرئيسية. تأخذ المؤشرات اللاتينية أ، ب، ج القيم 1، 2، المقابلة لإحداثيات الفضاء x 1، x 2 والتي ستكتب أيضًا كـ x، y . لذلك، فإن المقياس هو
-
(eq. 92)
يجب أن يلبي الحل المطلوب عدم المساواة
-
(eq. 93)
-
(eq. 94)
(تحدد هذه الشروط أن إحدى الوظائف a 2، b 2، c 2 صغيرة مقارنة بالوظيفتين الأخريين، وهو ما حدث أيضًا مع النماذج المتجانسة). عدم المساواة eq. 94 يعني أن المكونات a 3 صغيرة بمعنى أنه في أي نسبة من الإزاحات dx a و dz، يمكن حذف مصطلحات حاصل الضرب dx a dz في مربع عنصر الطول المكاني dl 2 . لذلك، فإن أول تقريب تقريبي للحل هو مقياس متري eq. 92 مع γ a 3 = 0: [note 22]
-
(eq. 95)
يمكن حساب مكونات موتر ريتشي
و
و
و
باستخدام eq. 95 والشرط eq. 93 أن جميع المصطلحات التي تحتوي على مشتقات بواسطة الإحداثيات x a صغيرة مقارنة بالمصطلحات ذات المشتقات بـ و z (نسبتها هي ~ γ 33 / γ ab ). بمعنى آخر، للحصول على معادلات التقريب الرئيسي، γ 33 و ab في eq. 95 كما لو أنها لا تعتمد على x a . التعيين
-
(eq. 96)
يتم الحصول على المعادلات التالية: [note 23]
-
(eq. 97)
-
(eq. 98)
-
(eq. 99)
يتم رفع المؤشر وخفضه هنا بمساعدة γ ab . الكميات
و λ هي الانقباضات
و
بواسطة
-
(eq. 100)
أما مكونات موتر ريتشي
و
، من خلال هذا الحساب فهي متطابقة صفر. في التقريب التالي (على سبيل المثال، مع مراعاة الصغير a 3 والمشتقات بواسطة x، y )، يحددان الكميتين a 3 بواسطة 33 و γ ab المعروفين بالفعل. eq. 97 تعطي
، وبالتالي،
-
(eq. 101)
حالات مختلفة ممكنة اعتمادًا على متغير G. في الحالة أعلاه، g 00 = γ 33
γ أب و
. الحالة N > 0 (الكمية N تشبه الوقت) تؤدي إلى تفردات زمنية ذات أهمية. استبدال في eq. 101 f 1 = 1/2 (ξ + z ) sin y، f 2 = 1/2 (ξ - z ) ينتج عن sin y G من النوع
-
(eq. 102)
هذا الاختيار لا يقلل من عمومية الاستنتاجات ؛ يمكن إثبات أن العمومية ممكنة (في التقريب الأول) فقط بسبب التحولات المتبقية المسموح بها للمتغيرات. عند N <0 (الكمية N تشبه الفضاء) يمكن استبدال G = z الذي يعمم مقياس أينشتاين-روزن المعروف. [52] عند N = 0 يصل المرء إلى مقياس موجة روبنسون – بوندي [53] الذي يعتمد فقط على + z أو فقط على ξ - z (راجع [37] ). العامل sin y في eq. 102 للمقارنة المريحة مع النماذج المتجانسة. مع الأخذ في الاعتبار eq. 102، المعادلات eq. 97 - eq. 99 يصبح
-
(eq. 103)
-
(eq. 104)
-
(eq. 105)
المعادلات الرئيسية هي eq. 103 تحديد مكونات γ ab ؛ إذن، يتم العثور على الوظيفة ψ من خلال تكامل بسيط لـ eq. 104 - eq. 105 . المتغير ξ يمر عبر القيم من 0 إلى ∞. حل eq. 103 تعتبر حدين، ξ
1 و
1. في القيم ξ كبيرة، يمكن للمرء أن نبحث عن الحل الذي يأخذ شكل 1 / √ξ التحلل:
-
(eq. 106)
بواسطة
-
(eq. 107)
(المعادلة 107 تحتاج إلى الشرط 102 ليكون صحيحاً). استبدال eq. 103 في eq. 106، يتم الحصول على الترتيب الأول
-
(eq. 108)
حيث الكميات a ac تشكل مصفوفة معكوسة للمصفوفة a ac . حل eq. 108 لديه الشكل
-
(eq. 109)
-
(eq. 110)
حيث l a، m a،، هي وظائف عشوائية للإحداثيات x، y مرتبطة بالشرط eq. 110 مشتق من eq. 107 . للعثور على شروط أعلى لهذا التحلل، من الملائم كتابة مصفوفة الكميات المطلوبة ab في النموذج
-
(eq. 111)
-
(eq. 112)
حيث الرمز ~ يعني تبديل المصفوفة. المصفوفة H متماثلة وأثرها صفر. عرض eq. 111 يضمن تناظر γ ab واستيفاء شرط eq. 102 . إذا تم استبدال exp H بـ 1، فسيحصل المرء من eq. 111 γ ab = ξ a ab مع a ab من eq. 109 . بمعنى آخر، المصطلح الأول لتحلل γ ab يتوافق مع H = 0 ؛ يتم الحصول على الشروط الأعلى من خلال تحلل القوى للمصفوفة H التي تعتبر مكوناتها صغيرة. تتم كتابة المكونات المستقلة للمصفوفة H بالشكل σ و بحيث
-
(eq. 113)
استبدال eq. 111 في eq. 103 وترك فقط المصطلحات الخطية بواسطة H، يشتق أحدهما لـ و
-
(eq. 114)
إذا حاول المرء إيجاد حل لهذه المعادلات مثل سلسلة فورييه بواسطة إحداثي z، فعندئذٍ بالنسبة لمعاملات السلسلة، كوظائف، يحصل المرء على معادلات Bessel. المصطلحات المقاربة الرئيسية للحل بشكل عام هي [note 24]
-
(eq. 115)
المعاملتان A و B هي وظائف معقدة عشوائية للإحداثيات x و y وتفي بالشروط اللازمة لـ σ و الحقيقيين ؛ التردد الأساسي ω هو دالة حقيقية تعسفية لـ x، y . الآن من eq. 104 - eq. 105 من السهل الحصول على الحد الأول من الوظيفة ψ:
-
(eq. 116)
(يختفي هذا المصطلح إذا كانت = 0 ؛ في هذه الحالة، المصطلح الرئيسي هو الخطي الوحيد لـ ξ من التحلل: ψ = ξ q ( x، y ) حيث q دالة موجبة [54] ).
لذلك، عند قيم الكبيرة، تتأرجح مكونات الموتر المتري γ ab عند تناقص على خلفية انخفاض بطيء ناتج عن تناقص عامل ξ في eq. 111 . وγ مكون 33 ه = ψ ينخفض بسرعة عن طريق وثيقة القانون إلى إكسب (ρ 2 ξ 2)؛ هذا يجعل من الممكن لشرط eq. 93 . [note 25]
التالي لتفرد بي كي إل النظر في الحالة ξ
1. التقريب الأول لحل eq. 103 خلال الافتراض (الذي أكدته النتيجة) أنه في هذه المعادلات يمكن استبعاد المصطلحات المتعلقة بالمشتقات بالإحداثيات:
-
(eq. 117)
هذه المعادلة مع الشرط eq. 102 يعطي
-
(eq. 118)
حيث λ a، μ a، s 1، s 2 هي وظائف تعسفية لجميع الإحداثيات الثلاثة x، y، z، المرتبطة بشروط أخرى
-
(eq. 119)
المعادلات eq. 104 - eq. 105 أعط الآن
-
(eq. 120)
المشتقات
، محسوبة بواسطة eq. 118، تتضمن شروطا ~ ξ 4 ثانية 1-2 و~ ξ 4 الصورة 2-2 بينما حيث غادر في eq. 117 ~ ξ −2 . لذلك، تطبيق eq. 103 بدلاً من eq. 117 مسموحًا بشروط s 1 > 0، s 2 > 0 ؛ ومن ثم 1 -
> 0.
وبالتالي، عند التذبذبات الصغيرة للوظائف، تتوقف γ ab بينما تبدأ الوظيفة γ 33 في الزيادة عند التناقص ξ. هذا هو وضع Kasner وعندما تتم مقارنة γ 33 مع γ ab، فإن التقريب أعلاه لا ينطبق.
من أجل التحقق من توافق هذا التحليل، قامت BKL بدراسة المعادلات = 0، = 0، وحساب المكونات γ a 3 منها، أكد أن eq. 94 يحدث. أظهرت هذه الدراسة [51] أنه في كلا المنطقتين المتقاربتين، كانت المكونات γ a 3 ~ 33 . لذلك، فإن صحة عدم المساواة eq. 93 يشير على الفور إلى صحة عدم المساواة eq. 94 .
يحتوي هذا الحل، كما ينبغي للحالة العامة للمجال في الفراغ، على أربع وظائف عشوائية للإحداثيات الفضائية الثلاثة x، y، z . في المنطقة ξ 1 هذه الوظائف هي، على سبيل المثال، 1، λ 2، μ 1، s 1 . في المنطقة ξ 1 يتم تعريف الوظائف الأربع بواسطة سلسلة فورييه عن طريق إحداثيات z من eq. 115 ذات معاملات هي دوال في x، y ؛ على الرغم من أن تحلل سلسلة فورييه (أو التكامل؟) يميز فئة خاصة من الوظائف، فإن هذه الفئة كبيرة بما يكفي لتشمل أي مجموعة فرعية محدودة من مجموعة جميع الشروط الأولية الممكنة.
يحتوي الحل أيضًا على عدد من الوظائف التعسفية الأخرى للإحداثيات x و y . تظهر مثل هذه الوظائف التعسفية ثنائية الأبعاد، بشكل عام، لأن العلاقات بين الوظائف ثلاثية الأبعاد في حلول معادلات أينشتاين تفاضلية (وليست جبرية)، تاركة جانباً المشكلة الأعمق حول المعنى الهندسي لهذه الوظائف. لم يحسب تفرد بي كي إل عدد الوظائف ثنائية الأبعاد المستقلة لأنه في هذه الحالة من الصعب التوصل إلى استنتاجات لا لبس فيها لأن الوظائف ثلاثية الأبعاد يتم تعريفها بواسطة مجموعة من الوظائف ثنائية الأبعاد (راجع [51] لمزيد من التفاصيل). [note 26]
أخيرًا، يستمر تفرد بي كي إل في إظهار أن الحل العام يحتوي على الحل الخاص الذي تم الحصول عليه أعلاه للنماذج المتجانسة.
استبدال النواقل الأساسية لمساحة متجانسة من نوع بيانكي من النوع IX في eq. 7 يأخذ مقياس الزمكان في هذا النموذج الشكل
-
(eq. 121)
عندما ج 2
أ 2، ب 2، يمكن للمرء أن يتجاهل ج 2 في كل مكان باستثناء المصطلح ج 2 دز 2 . للانتقال من الإطار المتزامن المستخدم في eq. 121 إلى إطار بشروط eq. 91، تم إجراء التحويل dt = cd ξ / 2 والاستبدال z → z / 2. بافتراض أن χ ≡ ln ( أ / ب )
1، يحصل المرء من eq. 121 في أول تقدير تقريبي:
-
(eq. 122)
وبالمثل، مع نواقل الأساس لمساحة متجانسة من النوع الثامن من بيانكي، يحصل المرء عليها
-
(eq. 123)
وفقًا لتحليل المساحات المتجانسة أعلاه، في كلتا الحالتين ab = ξ (تبسيط
= ξ 0 ) و من eq. 51 ؛ يتم إعطاء الوظيفة ج (ξ) بواسطة الصيغ eq. 53 eq. 61، على التوالي، للطرازين من النوعين التاسع والثامن. يتم الحصول على المقياس المتطابق للنوع الثامن من eq. 112، eq. 115، eq. 116 اختيار متجه ثنائي الأبعاد l a و m a بالشكل
-
(eq. 124)
والاستعاضة عنها
-
(eq. 125)
للحصول على مقياس النوع التاسع، يجب استبداله
-
(eq. 126)
(لحساب c (ξ) التقريب في eq. 116 غير كافٍ والمصطلح في خطي بمقدار ξ يتم حسابه [54] )
تم إجراء هذا التحليل للمساحة الفارغة. إن تضمين المادة لا يجعل الحل أقل عمومية ولا يغير خصائصه النوعية.[51][54]
أحد القيود ذات الأهمية الكبيرة للحل العام هو أن جميع الوظائف ثلاثية الأبعاد الواردة في المقاييس eq. 122 eq. 123 على فترة تغيير مميزة واحدة ومشتركة. هذا فقط يسمح بالتقريب في معادلات أينشتاين لجميع مشتقات المكونات المكانية المترية مع منتجات بسيطة من هذه المكونات بأرقام موجية مميزة مما ينتج عنه معادلات تفاضلية عادية من النوع الذي تم الحصول عليه للنموذج المتجانس من النوع IX. هذا هو سبب التطابق بين الحلول المتجانسة والحلول العامة.
ويترتب على ذلك أن كلاً من نموذج النوع التاسع وتعميمه يحتويان على وضع تذبذب بمقياس مكاني واحد بحجم تعسفي لم يتم اختياره من بين أمور أخرى بواسطة أي ظروف فيزيائية. ومع ذلك، فمن المعروف أنه في الأنظمة غير الخطية ذات درجات الحرية اللانهائية، يكون هذا الوضع غير مستقر ويتبدد جزئيًا إلى اهتزازات أصغر. في الحالة العامة للاضطرابات الصغيرة ذات الطيف التعسفي، سيكون هناك دائمًا بعض الذين تزيد اتساعهم من التغذية على إجمالي طاقة العملية. نتيجة لذلك، تظهر صورة معقدة للحركات متعددة المقاييس مع توزيع معين للطاقة وتبادل الطاقة بين التذبذبات ذات المقاييس المختلفة. لا يحدث ذلك فقط في الحالة التي يكون فيها تطور التذبذبات على نطاق صغير مستحيلًا بسبب الظروف المادية. بالنسبة للأخير، يجب أن يوجد بعض الطول المادي الطبيعي الذي يحدد الحد الأدنى للمقياس الذي تخرج فيه الطاقة من نظام بدرجات ديناميكية من الحرية (والتي، على سبيل المثال، تحدث في سائل مع لزوجة معينة). ومع ذلك، لا يوجد مقياس مادي فطري لحقل الجاذبية في الفراغ، وبالتالي، لا يوجد عائق أمام تطور التذبذبات للمقاييس الصغيرة بشكل تعسفي. [55]
الاستنتاجات
يصف تفرد بي كي إل التفردات في الحل الكوني لمعادلات أينشتاين التي لها طابع تذبذب معقد. على الرغم من أن هذه التفردات قد درست في المقام الأول على نماذج متجانسة مكانيًا، إلا أن هناك أسبابًا مقنعة لافتراض أن التفردات في الحل العام لمعادلات أينشتاين لها نفس الخصائص ؛ هذا الظرف يجعل نموذج بي كي إل مهمًا لعلم الكونيات.
أساس هذا البيان هو حقيقة أن الوضع التذبذب في نهج التفرد ناتج عن الاضطراب الفردي الذي يتسبب أيضًا في عدم الاستقرار في حل كاسنر المعمم. تأكيد عمومية النموذج هو البناء التحليلي لعصر طويل مع التذبذبات الصغيرة. على الرغم من أن هذا السلوك الأخير ليس عنصرًا ضروريًا للتطور المتري بالقرب من التفرد، إلا أنه يحتوي على جميع الخصائص النوعية الرئيسية: التذبذب المتري في بعدين مكانيين وتغيير رتيب في البعد الثالث مع اضطراب معين لهذا الوضع في نهاية بعض الوقت فترة. ومع ذلك، فإن التحولات بين عهود كاسنر في الحالة العامة للمقياس المكاني غير المتجانس لم يتم توضيحها بالتفصيل.
تم ترك المشكلة المرتبطة بالقيود المحتملة على هندسة الفضاء الناتجة عن التفرد جانبًا لمزيد من الدراسة. من الواضح منذ البداية، مع ذلك، أن نموذج بي كي إل الأصلي ينطبق على كل من المساحة المحدودة أو اللانهائية ؛ يتضح هذا من خلال وجود نماذج تفرد متذبذبة لكل من الزمكانات المغلقة والمفتوحة.
يعطي الوضع التذبذب لمقاربة التفرد جانبًا جديدًا لمصطلح "محدودية الوقت". بين أي لحظة محدودة من الزمن العالمي t واللحظة t = 0 يوجد عدد لا حصر له من التذبذبات. بهذا المعنى، تكتسب العملية طابعًا لا نهائيًا. بدلاً من الوقت t، يكون المتغير الأكثر ملاءمة لوصفه هو ln t الذي يتم من خلاله تمديد العملية .
تعتبر نظرية بي كي إل في التطور المتري في اتجاه تناقص الوقت متماثلة مع معادلات أينشتاين فيما يتعلق بعلامة الوقت بحيث يكون التطور المتري في اتجاه زيادة الوقت ممكنًا بشكل متساوٍ. ومع ذلك، فإن هاتين الحالتين تختلفان اختلافًا جوهريًا لأن الماضي والمستقبل ليسا متكافئين بالمعنى المادي. يمكن أن تكون التفردات المستقبلية ذات مغزى ماديًا فقط إذا كان ذلك ممكنًا في الظروف الأولية التعسفية الموجودة في اللحظة السابقة. لا يتوافق توزيع المادة والحقول في لحظة ما من تطور الكون بالضرورة مع الشروط المحددة المطلوبة لوجود حل خاص معين لمعادلات أينشتاين.
يرتبط اختيار الحلول المطابقة للعالم الحقيقي بالمتطلبات الفيزيائية العميقة التي يستحيل العثور عليها باستخدام نظرية النسبية الحالية فقط والتي يمكن العثور عليها كنتيجة للتوليف المستقبلي للنظريات الفيزيائية. وبالتالي، قد يتضح أن هذا الاختيار يفرد نوعًا خاصًا (مثل الخواص) من التفرد. ومع ذلك، فمن الطبيعي أن نفترض أنه بسبب طابعه العام، يجب أن يكون الوضع التذبذب هو السمة الرئيسية لمراحل التطور الأولية.
في هذا الصدد، فإن خاصية نموذج "مكسماستر" الموضحة بواسطة ميزنر، [56] ذات الصلة بانتشار الإشارات الضوئية، لها أهمية كبيرة. في النموذج الخواص، يوجد "أفق ضوئي"، مما يعني أنه لكل لحظة من الزمن، توجد مسافة أطول، يكون فيها تبادل الإشارات الضوئية، وبالتالي، الارتباط السببي، أمرًا مستحيلًا: لا يمكن للإشارة أن تصل إلى مثل هذه المسافات من أجل الوقت منذ التفرد t = 0.
يتم تحديد انتشار الإشارة بواسطة المعادلة ds = 0. في النموذج الخواص بالقرب من التفرد t = 0، يكون عنصر الفاصل الزمني
، أين
هو شكل تفاضلي مكاني مستقل عن الزمن. [37] الاستبدال
عائدات.
-
(eq. 127)
المسافة"
وصلت إليها الإشارة
-
(eq. 128)
نظرًا لأن η، مثل t، يمر عبر القيم التي تبدأ من 0، وحتى "اللحظة"، لا يمكن للإشارات أن تنتشر إلا على مسافة
التي تحدد المسافة الأبعد إلى الأفق.
يطرح وجود أفق ضوئي في النموذج الخواص مشكلة في فهم أصل الخواص الملحوظة حاليًا في الإشعاع المتبقي. وفقًا للنموذج المتناحي الخواص، فإن الخواص المتناحية الملحوظة تعني الخصائص المتناحية للإشعاع التي تأتي إلى المراقب من مناطق الفضاء التي لا يمكن ربطها سببيًا ببعضها البعض. يمكن أن يكون الوضع في نموذج التطور التذبذب بالقرب من التفرد مختلفًا.
على سبيل المثال، في النموذج المتجانس لفضاء النوع IX، تنتشر الإشارة في اتجاه تتغير فيه المقاييس لعصر طويل بقانون قريب من ~ t . مربع عنصر المسافة في هذا الاتجاه هو dl 2 = t 2
، والعنصر الخاص بالفاصل الزمني رباعي الأبعاد هو
. الاستبدال
يضع هذا في النموذج
-
(eq. 129)
وبالنسبة لانتشار الإشارة، يوجد معادلة من النوع eq. 128 مرة أخرى. الاختلاف المهم هو أن المتغير يعمل الآن من خلال القيم التي تبدأ من
(إذا كان المقياس eq. 129 صالحًا لجميع t بدءًا من t = 0).
لذلك، بالنسبة لكل "لحظة" معينة، تم العثور على فترات وسيطة كافية للإشارة لتغطية كل مسافة محدودة.
بهذه الطريقة، خلال حقبة طويلة، يتم فتح أفق ضوئي في اتجاه فضائي معين. على الرغم من أن مدة كل حقبة طويلة لا تزال محدودة، إلا أنه خلال مسار تطور العالم، تغيرت العصور عددًا لا حصر له من المرات في اتجاهات فضائية مختلفة. هذا الظرف يجعل المرء يتوقع أنه في هذا النموذج، من الممكن وجود علاقة سببية بين الأحداث في الفضاء بأكمله. بسبب هذه الخاصية، أطلق ميزنرعلى هذا الطراز "مكسماستر يونيفرس" باسم علامة تجارية لآلة خلط العجين.
مع مرور الوقت ويبتعد المرء عن التفرد، يزداد تأثير المادة على التطور المتري، الذي كان ضئيلاً في المراحل الأولى من التطور، تدريجياً ويصبح في النهاية مهيمناً. من المتوقع أن يؤدي هذا التأثير إلى "تماثل" تدريجي للفضاء، ونتيجة لذلك تقترب خصائصه من نموذج فريدمان الذي يصف بشكل مناسب الحالة الحالية للكون.
أخيرًا، يطرح تفرد بي كي إل مشكلة حول جدوى التفكير في "حالة فردية" لعالم به مادة كثيفة للغاية على أساس نظرية النسبية الحالية. يمكن توضيح التطبيق المادي لمعادلات أينشتاين في شكلها الحالي في هذه الظروف فقط في عملية التركيب المستقبلي للنظريات الفيزيائية، وبهذا المعنى لا يمكن حل المشكلة في الوقت الحاضر.
من المهم ألا تفقد نظرية الجاذبية نفسها تماسكها المنطقي (أي لا تؤدي إلى خلافات داخلية) مهما كانت كثافات المادة. بمعنى آخر، هذه النظرية غير مقيدة بالشروط التي تفرضها، والتي يمكن أن تجعل تطبيقها غير مقبول منطقيًا ومثيرًا للجدل في كثافات كبيرة جدًا ؛ يمكن أن تظهر القيود، من حيث المبدأ، فقط كنتيجة لعوامل "خارجية" لنظرية الجاذبية. هذا الظرف يجعل دراسة التفردات في النماذج الكونية مقبولة رسميًا وضرورية في إطار النظرية الحالية.
ملحوظات
- ^ The convention used by BKL is the same as in the Landau & Lifshitz (1988) book. The Latin indices run through the values 0, 1, 2, 3; Greek indices run through the space values 1, 2, 3. The metric gik has the signature (+ − − −); γαβ = −gαβ is the 3-dimensional space metric tensor. BKL use a system of units, in which the speed of light and the Einstein gravitational constant are equal to 1.
- ^ The expression for r is derived by logarithming the power coefficients in the metric: ln [t2pα(1/u)] = 2pα(1/u) ln t.
- ^ When (p1, p2, p3) = (0, 0, 1) the spacetime metric قالب:EquationNote with dl2 from قالب:EquationNote transforms to Galilean metric with the substitution t sh z = ζ, t ch z = τ, that is, the singularity is fictional and the spacetime is flat.
- ^ Here and below all symbols for vector operations (vector products, the operations rot, grad, etc.) should be understood in a very formal way as operations over the covariant components of the vectors l, m, n such that are performed in نظام إحداثي ديكارتي x1, x2, x3.
- ^ Here and below all symbols for vector operations (vector products, the operations rot, grad, etc.) should be understood in a very formal way as operations over the covariant components of the vectors l, m, n such that are performed in نظام إحداثي ديكارتي x1, x2, x3.
- ^ The convention used by BKL is the same as in the Landau & Lifshitz (1988) book. The Latin indices run through the values 0, 1, 2, 3; Greek indices run through the space values 1, 2, 3. The metric gik has the signature (+ − − −); γαβ = −gαβ is the 3-dimensional space metric tensor. BKL use a system of units, in which the speed of light and the Einstein gravitational constant are equal to 1.
- ^ Excepting the case (p1, p2, p3) = (0, 0, 1), in which the metric singularity is fictitious.
- ^ The constants λ, μ, ν are the so-called structural constants of the space movement group.
- ^ The convention used by BKL is the same as in the Landau & Lifshitz (1988) book. The Latin indices run through the values 0, 1, 2, 3; Greek indices run through the space values 1, 2, 3. The metric gik has the signature (+ − − −); γαβ = −gαβ is the 3-dimensional space metric tensor. BKL use a system of units, in which the speed of light and the Einstein gravitational constant are equal to 1.
- ^ In their exact form, the Einstein equations for homogeneous space contain, in general, 6 different functions of time γab(t) in the metric. The fact that in the present case a consistent system of exact equations is obtained for the metric which contains only 3 functions of time (γ11 = а2, γ22 = b2, γ33 = c2) is related to a symmetry that leads to the disappearance of 6 Ricci tensor components.
- ^ The asymptotic values of ατ, βτ, γτ at τ → −∞ can be found without fully solving قالب:EquationNote. It suffices to note that the first of these equations has a form of a "particle" moving in one dimension in the field of an exponential potential wall with α playing the role of a constant. In this analogy, the Kasner mode refers to a free movement with constant velocity ατ = Λp1. After reflection from the wall, the particle moves freely with velocity ατ = −Λp1. Also noting that from قالب:EquationNote ατ + βτ = const, and ατ + γτ = const, one can see that βτ and γτ take the values βτ = Λ(p2 − 2p1), γτ = Λ(p3 − 2p1).
- ^ Introduction of non-diagonal components of γab(t) imparts some new features to the BKL model: rotations of axes corresponding to the Kasner epoch powers; this problem is studied in Belinsky, Khalatnikov & Lifshitz (1971)
- ^ The constant in the sine argument, of course, is not necessarily the same as ξ0 in قالب:EquationNote and قالب:EquationNote; however, making them the same does not change in any way the solution character.
- ^ In a more precise calculation, a slowly changing logarithmic term appears in the sine argument, and a multiplier appears in front the exponent in the expression for с(ξ), see Belinsky, Khalatnikov & Lifshitz 1970.
- ^ If in قالب:EquationNote, one substitutes sh 2χ with 2χ and solves it for all values of ξ, one obtains χ = c1J0(ξ) + c2N0(ξ) where J0, N0 are Bessel functions of the I and II kind. This solution interpolates between the two limiting cases and allows to relate by an order of magnitude the constant parameters in قالب:EquationNote and قالب:EquationNote.
- ^ Since a, b, c have the dimension of length, their logarithms are defined only up to an additive constant which depends on the choice of the length units; in this sense قالب:EquationNote has a conditional meaning corresponding to a certain choice of the zero value of α, β, γ.
- ^ According to قالب:EquationNote, transitions are large with small |p1| (i. e. large u) and are ≈1/|p1| ~ u. But even in this case Δn ~ un |αn| un
- ^ Fixing the limits of the era according to eq. قالب:EquationNote is meaningful because in such case the era contains all epochs in which the third function, γ(t) decreases monotonously. If the era is defined by the sequence of u values from k + x to 1 + x, then the monotonous decrease of γ(t) will continue during the first epoch of the next era.
- ^ Epoch lengths are great in comparison to transitions between epochs. According to قالب:EquationNote transition lengths are great at small |p1| (i.e. large u) and are ∝ 1/|p1| ∝ u. But even in this case Δn ∝ un|αn| un.
- ^ قالب:EquationNote was known already to Gauss, and an equation of type قالب:EquationNote was considered in this connection by Rodion Kuzmin (see Gauss–Kuzmin distribution). Further information on the chaotic behaviour and entropy of continued fractions in Linas Vepstas. 2008. Entropy of Continued Fractions (Gauss-Kuzmin Entropy) نسخة محفوظة 2020-10-29 على موقع واي باك مشين.
- ^ The plot of the function P(δ) in Fig. 2 in Lifshitz, Lifshitz & Khalatnikov 1970 is incorrect for several reasons. Apparently some errors were admitted in preparing the program for numerical solution of the integral equation. Also a "forced" reduction of the values P(0) and P(1) was performed in view of the incorrect footnote in Lifshitz, Lifshitz & Khalatnikov 1970. The finite probability of the value δ = 0 does not mean the possibility of the initial amplitude of oscillation becoming zero (which would be in contradiction to the regular course of evolution shown in Fig. 4). From قالب:EquationNote δs+1 tends to zero with xs → 0 proportional to xs; but the amplitude is given by the product δs+1Ωs+1, which tends to a finite limit since the expression قالب:EquationNote contains a term with 1/xs.
- ^ Note that this metric allows arbitrary transformations of type ξ′ + z″ = f1 (ξ + z), ξ′ − z′ = f2 (ξ − z), x′a = fa (x1, x2).
- ^ The equation is a direct result of قالب:EquationNote–قالب:EquationNote if or . The case does not require a special treatment: it can be shown that the spacetime metric in this case converges (in first approximation) to Galilean.
- ^ It is possible to look for a solution in the form of Fourier integrals; this issue has not been studied in detail. Therefore, BKL do not require Fourier series decomposition as a mandatory condition for the coordinate dependence of functions σ and φ
- ^ Squared H terms in قالب:EquationNote result only in small (≈1/ξ) corrections in σ and φ. Calculation with cubic terms leads to appearance of a weak dependence of A, B from ξ that can be presented as an appearance of logarithmic phases in the oscillating factors in قالب:EquationNote. These calculations for the case ρ = 0 are given in Belinsky & Khalatnikov (1970) (cf. the analogous situation for homogeneous models, Belinsky, Khalatnikov & Lifshitz (1970)).
- ^ The regular decomposition of the general solution of Einstein equations contains (in addition to the four three-dimensional functions) three independent functions of two coordinates (cf. Petrov 1969; Lifshitz & Khalatnikov (1963))
مراجع
- ^ Garfinkle، David (2007). "Of singularities and breadmaking". Einstein Online. Band 03: 03–1014. مؤرشف من الأصل في 2007-08-10. اطلع عليه بتاريخ 2020-10-15.
{{استشهاد بدورية محكمة}}:|archive-date=/|archive-url=timestamp mismatch (مساعدة) - ^ أ ب ت Belinsky, Khalatnikov & Lifshitz 1970
- ^ Demaret, Henneaux & Spindel 1985.
- ^ Demaret et al. 1986.
- ^ Demaret, de Rop & Henneaux 1989.
- ^ Damour & Henneaux 2000.
- ^ Damour et al. 2001.
- ^ Damour, Henneaux & Nicolai 2003.
- ^ Kac 1983.
- ^ Damour 2015.
- ^ Henneaux, Persson & Spindel 2008.
- ^ أ ب ت ث ج ح Lifshitz & Khalatnikov 1963
- ^ أ ب Landau & Lifshitz 1988
- ^ Lifshitz & Khalatnikov 1961a.
- ^ Lifshitz & Khalatnikov 1961b.
- ^ أ ب Lifshitz, Sudakov & Khalatnikov 1961
- ^ Hawking 1965.
- ^ Hawking & Ellis 1968.
- ^ Geroch 1966.
- ^ أ ب Ashtekar, Henderson & Sloan 2011
- ^ Barrow & Tipler 1979.
- ^ Barrow & Tipler 1981.
- ^ أ ب Berger 2002
- ^ Garfinkle 2004.
- ^ Berger & Moncrief 1993.
- ^ Berger et al. 1998.
- ^ Weaver, Isenberg & Berger 1998.
- ^ Andersson & Rendall 2001.
- ^ Damour et al. 2002.
- ^ Berger & Moncrief 1998.
- ^ Berger & Moncrief 2000.
- ^ Garfinkle 2007.
- ^ Saotome, Akhoury & Garfinkle 2010.
- ^ Kasner 1921.
- ^ Rugh 1994.
- ^ Bini, Cherubini & Jantzen 2007.
- ^ أ ب ت Landau & Lifshitz 1988.
- ^ Landau & Lifshitz 1987.
- ^ Misner, Thorne & Wheeler 1973.
- ^ Nelson 1981.
- ^ Belinsky & Khalatnikov 1966.
- ^ Khalatnikov & Lifshitz 1970.
- ^ أ ب Belinsky & Khalatnikov 1969a
- ^ أ ب Lifshitz & Khalatnikov 1970
- ^ أ ب Belinsky, Khalatnikov & Lifshitz 1970.
- ^ Lifshitz & Khalatnikov 1963.
- ^ Taub 1951.
- ^ أ ب ت ث Lifshitz, Lifshitz & Khalatnikov 1970
- ^ أ ب Khalatnikov et al. 1985
- ^ Chernoff & Barrow 1983.
- ^ أ ب ت ث Belinsky & Khalatnikov 1970
- ^ Einstein & Rosen 1937.
- ^ Bondi, Pirani & Robinson 1959.
- ^ أ ب ت Belinsky & Khalatnikov 1969b
- ^ Belinsky 1992.
- ^ Misner 1969.
فهرس
- Andersson، Lars؛ Rendall، Alan D. (2001). "Quiescent cosmological singularities". Communications in Mathematical Physics. ج. 218 ع. 3: 479–511. arXiv:gr-qc/0001047. Bibcode:2001CMaPh.218..479A. DOI:10.1007/s002200100406. S2CID:16167683.
- Ashtekar، Abhay؛ Henderson، Adam؛ Sloan، David (2011). "Hamiltonian formulation of the Belinskii-Khalatnikov-Lifshitz conjecture". فيزيكال ريفيو. ج. 83 ع. 8: 084024. arXiv:1102.3474. Bibcode:2011PhRvD..83h4024A. DOI:10.1103/PhysRevD.83.084024.
- Barrow، John D.؛ Tipler، Frank J. (1979). "Analysis of the generic singularity studies by Belinskii, Khalatnikov, and Lifshitz". Physics Reports. ج. 56 ع. 7: 371–402. Bibcode:1979PhR....56..371B. DOI:10.1016/0370-1573(79)90097-8.
- Barrow، John D.؛ Tipler، Frank J. (1981). "Generic singularity studies revisited". Physics Letters. ج. 82A ع. 9: 441–445. DOI:10.1016/B978-0-08-036364-6.50050-8.
- Belinsky، Vladimir A.؛ Khalatnikov، I.M. (1966). "A general solution of the gravitational equations with a simultaneous fictitious singularity". JETP. ج. 49 ع. 3: 1000. Bibcode:1966JETP...22..694B.
- Belinsky، Vladimir A.؛ Khalatnikov، I.M. (1969). "On the nature of the singularities in the general solution of the gravitational equations". JETP. ج. 56: 1700.
- Belinsky، Vladimir A.؛ Khalatnikov، I.M. (1969). "General solution of the gravitational equations with a physical singularity". JETP. ج. 57: 2163.
- Belinsky، Vladimir A.؛ Khalatnikov، Isaak M.؛ Lifshitz، Evgeny M. (1970). "Колебательный режим приближения к особой точке в релятивистской космологии". Uspekhi Fizicheskikh Nauk. ج. 102 ع. 11: 463–500. Bibcode:1970UsFiN.102..463B. DOI:10.3367/ufnr.0102.197011d.0463.; English translation in Belinskii، V.A.؛ Khalatnikov، I.M.؛ Lifshitz، E.M. (1970). "Oscillatory Approach to a Singular Point in the Relativistic Cosmology". Advances in Physics. ج. 19 ع. 80: 525–573. Bibcode:1970AdPhy..19..525B. DOI:10.1080/00018737000101171.
- Belinsky، Vladimir A.؛ Khalatnikov، Isaak M. (1970). "General solution of the gravitational equations with a physical oscillatory singularity". JETP. ج. 59: 314. Bibcode:1971JETP...32..169B.
- Belinsky، Vladimir A.؛ Khalatnikov، I.M.؛ Lifshitz، E.M. (1971). "The oscillatory mode of approach to a singularity in homogeneous cosmological models with rotating axes". JETP. ج. 60 ع. 6: 1969–1979.
- Belinsky، V.A. (1992). "Turbulence of a Gravitational Field near a Cosmological Singularity". JETP Letters. ج. 56 ع. 9: 437–440.
- Belinski، Vladimir؛ Henneaux، Marc (2018). The Cosmological Singularity. مطبعة جامعة كامبريدج. arXiv:1404.3864. DOI:10.1017/9781107239333. ISBN:978-1-107-04747-1.
- Berger، Beverly؛ Moncrief، Vincent (1993). "Numerical investigation of cosmological singularities". Physical Review D. ج. 48 ع. 10: 4676–4687. arXiv:gr-qc/9307032. Bibcode:1993PhRvD..48.4676B. DOI:10.1103/PhysRevD.48.4676. PMID:10016121. S2CID:450414.
- Berger، Beverly K.؛ Moncrief، Vincent (1998). "Numerical evidence that the singularity in polarized U(1) symmetric cosmologies on T3 × R is velocity dominated". Physical Review D. ج. 57 ع. 12: 7235–7240. arXiv:gr-qc/9801078. Bibcode:1998PhRvD..57.7235B. DOI:10.1103/PhysRevD.57.7235. S2CID:119539705.
- Berger، Beverly؛ Garfinkle، David؛ Isenberg، James؛ Moncrief، Vincent؛ Weaver، Marsha (1998). "The singularity in generic gravitational collapse is spacelike, local, and oscillatory". Modern Physics Letters A. ج. 13 ع. 19: 1565–1573. arXiv:gr-qc/9805063. Bibcode:1998MPLA...13.1565B. DOI:10.1142/S0217732398001649. S2CID:118889710.
- Berger، Beverly K.؛ Moncrief، Vincent (2000). "Signature for local Mixmaster dynamics in U(1) symmetric cosmologies". Physical Review D. ج. 62 ع. 123501: 123501. arXiv:gr-qc/0006071. Bibcode:2000PhRvD..62l3501B. DOI:10.1103/PhysRevD.62.123501. S2CID:10389665.
- Berger، Beverly K (2002). "Numerical Approaches to Spacetime Singularities". Living Reviews in Relativity. ج. 5 ع. 1: 1. arXiv:gr-qc/0201056. Bibcode:2002LRR.....5....1B. DOI:10.12942/lrr-2002-1. PMC:5256073. PMID:28179859.
- Bini، Donato؛ Cherubini، Christian؛ Jantzen، Robert (2007). "The Lifshitz-Khalatnikov Kasner index parametrization and the Weyl tensor". Il Nuovo Cimento B. ج. 122 ع. 5: 521–536. arXiv:0710.4902. Bibcode:2007NCimB.122..521B. DOI:10.1393/ncb/i2007-10396-4. S2CID:15854390.
- Bini، Donato؛ Cherubini، Christian؛ Geralico، Andrea؛ Jantzen، Robert T. (2009). "Electrocardiogram of the Mixmaster Universe". Classical and Quantum Gravity. ج. 26 ع. 2: 025012. arXiv:0808.0828. Bibcode:2009CQGra..26b5012B. DOI:10.1088/0264-9381/26/2/025012. S2CID:14552653.
- Bondi، Herman؛ Pirani، F.A.E.؛ Robinson، I. (1959). "Gravitational Waves in General Relativity. III. Exact Plane Waves". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. ج. 251 ع. 1267: 519–533. Bibcode:1959RSPSA.251..519B. DOI:10.1098/rspa.1959.0124. JSTOR:100727. S2CID:122766998.
- Chernoff، David F.؛ Barrow، J.D. (1983). "Chaos in the Mixmaster Universe". Physical Review Letters. ج. 50 ع. 2: 134–137. Bibcode:1983PhRvL..50..134C. DOI:10.1103/PhysRevLett.50.134.
- Damour، Thibault؛ Henneaux، Marc (2000). "Chaos in superstring cosmology". Physical Review Letters. ج. 85 ع. 5: 920–923. arXiv:hep-th/0003139. Bibcode:2000PhRvL..85..920D. DOI:10.1103/PhysRevLett.85.920. PMID:10991439. S2CID:10752273.
- Damour، Thibault؛ Henneaux، Marc؛ Julia، Bernard؛ Nicolai، Hermann (2001). "Hyperbolic Kac–Moody algebras and chaos in Kaluza-Klein models". Physics Letters B. ج. 509 ع. 3–4: 323–330. arXiv:hep-th/0103094. Bibcode:2001PhLB..509..323D. DOI:10.1016/S0370-2693(01)00498-1. S2CID:16964946.
- Damour، Thibault؛ Henneaux، Marc؛ Nicolai، Hermann (2003). "Cosmological billiards". Classical and Quantum Gravity. ج. 20 ع. 9: R145–R200. CiteSeerX:10.1.1.262.7733. DOI:10.1088/0264-9381/20/9/201.
- Damour، Thibault؛ Henneaux، Marc؛ Rendall، Alan D.؛ Weaver، Marsha (2002). "Kasner-like behaviour for subcritical Einstein-matter systems". Annales Henri Poincaré. ج. 3 ع. 6: 1049–1111. arXiv:gr-qc/0202069. Bibcode:2002AnHP....3.1049D. DOI:10.1007/s000230200000. S2CID:17092394.
- Demaret، Jacques؛ Henneaux، Marc؛ Spindel، Philipe (1985). "Non-oscillatory behaviour in vacuum Kaluza–Klein cosmologies". Physics Letters. ج. 164B ع. 1–3: 27–29. Bibcode:1985PhLB..164...27D. DOI:10.1016/0370-2693(85)90024-3.
- Demaret، Jacques؛ Hanquin، Jean-Luc؛ Henneaux، Marc؛ Spindel، Philipe؛ Taormina، Anna (1986). "The fate of the Mixmaster behaviour in vacuum inhomogeneous Kaluza-Klein cosmological models". Physics Letters B. ج. 175 ع. 2: 129–132. Bibcode:1986PhLB..175..129D. DOI:10.1016/0370-2693(86)90701-X.
- Demaret، Jacques؛ de Rop، Yves؛ Henneaux، Marc (1989). "Are Kaluza-Klein models of the Universe chaotic?". International Journal of Theoretical Physics. ج. 28 ع. 9: 1067–1079. Bibcode:1989IJTP...28.1067D. DOI:10.1007/BF00670349. S2CID:121065247.
- Einstein، Albert؛ Rosen، Nathan (1937). "On gravitational waves". معهد فرانكلين. ج. 223 ع. 1: 43–54. Bibcode:1937FrInJ.223...43E. DOI:10.1016/S0016-0032(37)90583-0.
- Frasca، Marco (2006). "Strong coupling expansion for general relativity". International Journal of Modern Physics D. ج. 15 ع. 9: 1373–1386. arXiv:hep-th/0508246. Bibcode:2006IJMPD..15.1373F. DOI:10.1142/S0218271806009091. S2CID:15369171.
- Garfinkle، David (2004). "Numerical Simulations of Generic Singularities". Phys. Rev. Lett. ج. 93 ع. 16: 161101. arXiv:gr-qc/0312117. Bibcode:2004PhRvL..93p1101G. DOI:10.1103/PhysRevLett.93.161101. PMID:15524970. S2CID:37917240.
- Garfinkle، David (2007). "Numerical simulations of general gravitational singularities". Classical and Quantum Gravity. ج. 24 ع. 12: 295–306. arXiv:0808.0160. Bibcode:2007CQGra..24S.295G. DOI:10.1088/0264-9381/24/12/S19. S2CID:16899122.
- Geroch، Robert P. (1966). "Singularities in Closed Universes". Physical Review Letters. ج. 17 ع. 8: 445–447. Bibcode:1966PhRvL..17..445G. DOI:10.1103/PhysRevLett.17.445.
- Hawking، Stephen W. (1965). "Occurrence of Singularities in Open Universes". Physical Review Letters. ج. 15 ع. 17: 689–690. Bibcode:1965PhRvL..15..689H. DOI:10.1103/PhysRevLett.15.689.
- Hawking، Stephen W.؛ Ellis، G.F.R. (1968). "The Cosmic Black-Body Radiation and the Existence of Singularities in Our Universe". المجلة الفيزيائية الفلكية. ج. 152: 25. Bibcode:1968ApJ...152...25H. DOI:10.1086/149520.
- Heinzle، J. Mark؛ Uggla، Claes؛ Röhr، Niklas (2009). "The cosmological billiard attractor". Adv. Theor. Math. Phys. ج. 13 ع. 2: 293–407. arXiv:gr-qc/0702141. Bibcode:2007gr.qc.....2141H. DOI:10.4310/ATMP.2009.v13.n2.a1. S2CID:119470976.
- Henneaux، Marc؛ Persson، Daniel؛ Spindel، Philippe (2008). "Spacelike Singularities and Hidden Symmetries of Gravity". Living Reviews in Relativity. ج. 11 ع. 1: 1. arXiv:0710.1818. Bibcode:2008LRR....11....1H. DOI:10.12942/lrr-2008-1. PMC:5255974. PMID:28179821.
- Kac، Victor G. (1983). Infinite dimensional Lie algebras: an introduction. Progress in Mathematics. Basel: Birkhäuser. ج. 44. ص. 245. DOI:10.1007/978-1-4757-1382-4. ISBN:9780817631185.
- Kasner، Edward (1921). "Geometrical Theorems on Einstein's Cosmological Equations". American Journal of Mathematics. ج. 43 ع. 4: 217–221. Bibcode:1921AmJM...43..217K. DOI:10.2307/2370192. JSTOR:2370192.
- Khalatnikov، Isaak M.؛ Lifshitz، E.M.؛ Khanin، K.M.؛ Shchur، L.N.؛ Sinai، Ya.G. (1985). "On the stochasticity in relativistic cosmology". Journal of Statistical Physics. ج. 38 ع. 1–2: 97–114. Bibcode:1985JSP....38...97K. DOI:10.1007/BF01017851. S2CID:120521834.
- Khalatnikov، Isaak M.؛ Kamenshchik، Aleksander Yu. (2008). "Lev Landau and the problem of singularities in cosmology". Physics-Uspekhi. ج. 51 ع. 6: 609–616. arXiv:0803.2684. Bibcode:2008PhyU...51..609K. DOI:10.1070/PU2008v051n06ABEH006550. S2CID:14878079.
- Khalatnikov، I.M.؛ Lifshitz، E.M. (1970). "General Cosmological Solution of the Gravitational Equations with a Singularity in Time". Physical Review Letters. ج. 24 ع. 2: 76. Bibcode:1970PhRvL..24...76K. DOI:10.1103/PhysRevLett.24.76.
- Landau، Lev D.؛ Lifshitz، Evgeny M. (1988). Classical Theory of Fields. Course of Theoretical Physics (ط. 7th). Moscow: Nauka. ج. 2. ISBN:978-5-02-014420-0.
- Landau، Lev D.؛ Lifshitz، Evgeny M. (1987). Fluid Mechanics. Course of Theoretical Physics (ط. 2nd). Butterworth-Heinemann. ج. 6. ISBN:978-0-08-033933-7.
- Lifshitz، Evgeny M.؛ I.M. Khalatnikov (1961). "On the singularities of cosmological solutions of the gravitational equations.I". JETP. ج. 39: 149.
- Lifshitz، Evgeny M.؛ I.M. Khalatnikov (1961). "On the singularities of cosmological solutions of the gravitational equations.II". JETP. ج. 39: 800.
- Lifshitz، Evgeny M.؛ Sudakov، V.V.؛ Khalatnikov، I.M. (1961). "Singularities of cosmological solutions of the gravitational equations.III". JETP. ج. 40: 1847.; Physical Review Letters, 6, 311 (1961)
- Lifshitz، Evgeny M.؛ Khalatnikov، Isaak M. (1963). "Проблемы релятивистской космологии". Uspekhi Fizicheskikh Nauk. ج. 80 ع. 7: 391–438. DOI:10.3367/UFNr.0080.196307d.0391.; English translation in Lifshitz, E.M.؛ Khalatnikov، I.M. (1963). "Problems in the Relativistic Cosmology". Advances in Physics. ج. 12 ع. 46: 185. Bibcode:1963AdPhy..12..185L. DOI:10.1080/00018736300101283.
- Lifshitz، Evgeny M.؛ Khalatnikov، Isaak M. (1970). "Oscillatory mode of approach to a singularity in the open cosmological model". JETP Letters. ج. 11: 200–203.
- Lifshitz، E.M.؛ Lifshitz، I.M.؛ Khalatnikov، I.M. (1970). "Asymptotic analysis of oscillatory mode of approach to a singularity in homogeneous cosmological models". JETP. ج. 59: 322.
- Misner، Ch. W. (1969). "Mixmaster Universe". Physical Review Letters. ج. 22 ع. 20: 1071–1074. Bibcode:1969PhRvL..22.1071M. DOI:10.1103/PhysRevLett.22.1071.
- Misner، Charles W.؛ Thorne، Kip S.؛ Wheeler، John Archibald (1973). Gravitation. San Francisco: W.H. Freeman. ص. 564. ISBN:978-0-7167-0334-1.
- Nelson، Robert A. (1981). "Coordinate-dependent 3 + 1 formulation of the General Relativity equations for a perfect fluid". General Relativity and Gravitation. ج. 13 ع. 6: 569–580. Bibcode:1981GReGr..13..569N. DOI:10.1007/BF00757243. S2CID:122196359.
- Penrose، Roger (1965). "Gravitational Collapse and Space-Time Singularities". Physical Review Letters. ج. 14 ع. 3: 57–59. Bibcode:1965PhRvL..14...57P. DOI:10.1103/PhysRevLett.14.57.
- Petrov، Alexey Z. (1969). Einstein Spaces. Oxford: Pergamon Press. ISBN:978-0-08-012315-8.
- Rugh، Svend E. (1994). "Chaos in the Einstein Equations -- characterization and importance?". Deterministic Chaos in General Relativity. Kananaskis, Alberta, Canada: Springer Science+Business Media New York. ص. 359–422. DOI:10.1007/978-1-4757-9993-4. ISBN:978-1-4757-9995-8.
- Saotome، Ryo؛ Akhoury، Ratindranath؛ Garfinkle، David (2010). "Examining gravitational collapse with test scalar fields". Classical and Quantum Gravity. ج. 27 ع. 165019: 165019. arXiv:1004.3569. Bibcode:2010CQGra..27p5019S. DOI:10.1088/0264-9381/27/16/165019. S2CID:55229333.
- Taub، A.H. (1951). "Empty space-times admitting a three parameter group of motions". حوليات الرياضيات. Second Series. ج. 53 ع. 3: 472–490. Bibcode:1951AnMat..53..472T. DOI:10.2307/1969567. ISSN:0003-486X. JSTOR:1969567. MR:0041565.
- Thorne، Kip (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W W Norton. ISBN:978-0-393-31276-8.]؛ Kip Thorne (2015). Geometrodynamics: The Nonlinear Dynamics of Curved Spacetime (Video lecture). 28:00–41:00min: The Van Leer Jerusalem Institute.
{{استشهاد بوسائط مرئية ومسموعة}}: صيانة الاستشهاد: مكان (link) - Uggla، Claes؛ van Elst، Henk؛ Wainwright، John؛ Ellis، George F.R. (2003). "Past attractor in inhomogeneous cosmology". فيزيكال ريفيو. ج. 68 ع. 10: 103502. arXiv:gr-qc/0304002. Bibcode:2003PhRvD..68j3502U. DOI:10.1103/PhysRevD.68.103502. S2CID:53635765.
- Weaver، Marsha؛ Isenberg، James؛ Berger، Beverly K. (1998). "Mixmaster behavior in inhomogeneous cosmological spacetimes". Physical Review Letters. ج. 80 ع. 14: 2984–2987. arXiv:gr-qc/9712055. Bibcode:1998PhRvL..80.2984W. DOI:10.1103/PhysRevLett.80.2984. S2CID:119467400.
- Damour، Thibault (19 نوفمبر 2015). The Structure of Cosmological Singularities (Video lecture). Institut Henri Poincaré.
