|
تضامنًا مع حق الشعب الفلسطيني |
تضاؤل أسي

في الفيزياء النووية والإلكترونيات يقال عن كمية أنها تتحلل أسيـّا أو تضمحل أسيـّا (بالإنجليزية:exponential decay) عندما يكون معدل اضمحلالها متناسبا مع كميتها.[1] ويمكن التعبير عن عملية طبيعية كهذه بالمعادلة التفاضلية الآتية، حيث N الكمية (أو عدد ذرات) و (λ (lambda عدد صحيح يسمى ثابت التحلل:
وحل تلك المعادلة (أنظر حل المعادلات التفاضلية) تعطينا معادلة الدالة الأسية للأساس الطبيعي e :
حيث:
- N(t) الكمية عند الزمن t,
- و N0 = N(0) الكمية الابتدائية عند الزمن t = 0.
قياس ثابت التحلل
متوسط العمر
إذا كانت الكمية المتحللة مكونة من عدد من الذرات، فيمكن حساب متوسط الزمن الذي تبقى فيه الذرة على حالها بدون تحلل. وتسمي متوسط الزمن هذا «متوسط العمر» . والعلاقة بين متوسط العمر ومعدل التحلل هي:
ويسمى متوسط العمر أيضا ثابت زمني للاضمحلال ، وهو أحد مكونات أس الثابت الطبيعي e :
وهو يعطي الزمن الذي يضمحل أو يتحلل فيه النظام بنسبة الثابت الطبيعي e .
كما يمكن كتابة معادلة التحلل في صورة أخرى تستعمل كثيرا - كما يرى أسفله - وهي تعطي الحل في حالة اختيار أساس لأس مساويا 2 بدلا عن e. وذلك الحل يمثل حالة تساوي زمن الاضمحلال بزمن نصف العمر.
(ملحوظة 1 : أس الثابت الطبيعي يكون «دائما» عددا مطلقا (لا وحدات له)، فنجد فيه ووحدتها ثانية مثلا وt ووحدتها ثانية أيضا، فيكون الكسر /tعددا مطلقا.)
(ملحوظة 2: الأس له إشارة سالبة، مما يعنى أن الدالة في تناقص (اضمحلال). وفي بعض الحالات تكون إشارة الأس موجبة، وبالتالي تصبح قيمة الدالة في تزايد. تلك حالة تكوّن نجم من سحابة غبار كوني حيث يجمع مادة من حوله وتتزايد كتلته طبقا لدالة أسية موجبة الأس، حتي يبدأ فيه التفاعل النووي ويصبح نجما مضيئا.)
عمر النصف
من الخواص التسهيلية للتحلل الإسي للأساس e حساب الزمن الذي تتحلل أو تضمحل خلاله الكمية إلى نصف مقدارها الأولي. ويسمى ذلك الزمن نصف العمر، ويرمز له عادة بالرمز t1/2. ويمكن كتابة نصف العمر بعلاقته بثابت التحلل، كالآتي:
وعند التعويض بتلك المعادلة عن في المعدلة الأسية أعلاه نحصل على المعادلة:
وعندما تكون t = تصبح 2−1 = 1/2، أي تتحلل نصف الكمية الابتدائية. وكذلك بعد مرور 3 فترات من نصف العمر سيتبقى من الكمية الابتدائية الكمية 1/23 = 1/8.
وهذا معناه أن متوسط العمر يساوي نصف العمر مقسوما على اللوغاريتم الطبيعي ln2 :
وعلى سبيل المثال يبلغ عمر النصف للبولونيوم-210 المشع 138 يوم ويبلغ متوسط العمر له 200 يوم.
حل المعادلة التفاضلية
المعادلة التي تصف التحلل الأسي (تحلل أسي لأساس الثابت الطبيعي e):
أو:
بإجراء التكامل نحصل على:
حيث:
C ثابت التكامل.
وبالتالي:
نعوض عن عن طريق حل المعادلة عند الزمن الابتدائي حيث أن الكمية الابتدائية كانت عند الزمن الابتدائي .
تلك هي المعادلة الشائعة الاستخدام لوصف التحلل الأسي. وتعطى وحدات ثابت التحلل math> s−1.
استنتاج متوسط العمر
نفترض مجموعة من الذرات تتحلل باستمرار حتى تتحلل كلها بالكامل، فيكون متوسط العمر هو الزمن المتوقع لكي تتحلل إحدى الذرات في المجموعة. أي انه إذا كان عمر الذرة الواحدة من المجموعة هو الزمن بين الزمن المرجعي وزمن تحلل الذرة يكون متوسط العمر عبارة عن المتوسط الحسابي لعمر الذرات.
نبدأ بالمعادلة الأصلية للمجموعة:
نستخدم c كعدد توحيد normalzation ، يستخدم لمساواة الكمية بالواحد.
- أو:
يتبين أن التحلل الأسي هو مضاعفات (غير متجهة) للتوزيع الأسي، أي أن عمر الذرات تكون موزعة توزيعا أسيا يتميز بقيمة متوقعة، ويمكننا حسابها عن طريق إجراء التكامل الجزئي:
عمليات تحلل متوازية
تتحلل بعض العناصر المشعة في عمليات متوازية كل منها له عمر النصف الخاص به، وتسمى تلك العمليات «قنوات التحلل» وهي تسير جميعها في نفس الوقت.
يكون المعدل الكلي لتحلل الكمية N هو مجموع قنوات التحلل، أي أنه في حالة التحلل من خلال عمليتين، يمكن كتابة:
وحل تلك المسألة قد أجريناه في فصل آخر أعلاه، حيث عاملنا المجموع كثابت تحلل كلي جديد .
وبما أن ، مجموع ل فيمكن تعيينها من s:
وعلى ذلك فيمكن القول بأن متوسط العمر لعدة قنوات للتحلل هو المتوسط التوافقي لمتوسطات الأعمار المرتبطة لكل عملية تحلل على حدة مقسومة على عدد العمليات.
وبما أن أنصاف الأعمار تختلف عن متوسط العمر بثابت معين فإن نفس المعادلات تبقى سارية على نصف العمرين المذكورين، أي أن:
حيث:
- مجموع نصفي العمر للعملية
- عمر النصف للتحلل الأول،
- و عمر النصف للتحلل الثاني.
ولكتابة المعادلة باستخدام ثابتي التحلل، يصبح عمر النصف الكلي
موصوفا بالمعادلة:
وفي حالة تحلل يجري فيها ثلاثة من العمليات متزامنين فيمكن حساب عمر النصف الكلي كما أوضحانا أعلاه عن طريق حساب المتوسط التوافقي لمتوسطات الأعمار الفردية:
ظواهر تحكمها الدالة الأسية
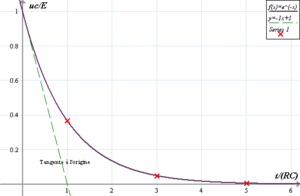
- تتحلل العناصر المشعة طبقا للدالة الأسية كما رئينا أعلاه
- إذا تلامس جسم ساخن بجسم بارد تنتقل الحرارة بينهما طبقا للدالة الأسية عنما يجري ذلك بسرعة بطيئة، قانون نيوتن للتبريد.
- يعتمد معدل سير التفاعل الكيميائي على تركيز أحد المواد الداخلة في التفاعل أو تركيز كلاهما. تلك الأنواع من التفاعلات تحكمها دالة أسية. كذلك تفاعل الإنزيمات وتفاعل المحفزات تسير طبقا لدالة أسية.
- يقل الضغط الجوي بالارتفاع عن سطح الأرض طبقا لدالة أسية، ويبلغ معدل انخفاض الضغط بالرتفاع 12% لكل 1000 متر.
- تنخفض شحنة مكثف كهربائي ذو سعة كهربائية C طبقا لدالة أسية في حالة ثبات المقاومة R
ويكون مقدار الثابت الزمني τ للعملية مساويا R C ، وزمن الشحن إلى النصف مساويا R C ln2.
وفي حالة تفريغ مكثف كهربي عبر عدة مقاومات موصلة على التوازي فهذا مثال على عمليات اضمحلال متتابعة حيث تمصل كل مقاومة عملية منفردة. وفي الواقع فإن معادلات توصيل مقاومتين على التوالي أو على التوازي فإنما هي مناظرة لمعادلات التحلل الأسي عن طريق عمليتين.
- تضمحل بعض الاهتزازات طبقا لدالة أسية
- في الصيدلة وعلم السموم فقد وجد أن أدوية عديدة تتفاعل في الجسم طبقا لدالة أسية. وتعطي كل من «عمر النصف ألفا» و«عمر النصف بيتا» في الطب معدل انتشار مادة في الجسم ومعدل اضمحلالها.
- تتغير شدة الموجات الكهرومغناطيسية مثل الضوء وأشعة إكس أو أشعة غاما في وسط يمتصها طبقا لدالة أسية تعتمد على مدى تعمقها في الوسط.
مراجع
- ^ Leike، A. (2002). "Demonstration of the exponential decay law using beer froth". European Journal of Physics. ج. 23: 21. Bibcode:2002EJPh...23...21L. DOI:10.1088/0143-0807/23/1/304.