|
تضامنًا مع حق الشعب الفلسطيني |
منظومة رصينة
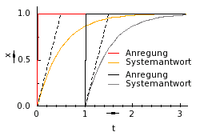
النظام المستقل زمنيا[1] أو المنظومة الرصينة أو المنظومة اللامتغيرة زمنيا هي المنظومة التي لا تعتمد استجابتها لأي دخل على متغير الزمن أي أنه يظهر التصرف ذاته في مختلف الأزمان. ومن الأمثلة البسيطة على المنظومات الرصينة المصباح والحنفية وغيرها من المنظومات التي تعمل بنفس الطريقة بغض النظر عن عامل الزمن. على عكس مثلا الطائرة التي تختلف خصائصها حين الإقلاع عن خصائصها حين التحليق عن خصائصها حين الهبوط مع الأخذ بالاعتبار تناقص كمية الوقود مع الزمن. أما في الرياضيات ونظرية التحكم فالمنظومة الرصينة هي المنظومة التي لا تتأثر دالة تحويلها بمتغير الزمن أو بمعنى آخر، تكون أي منظومة رصينة إذا كانت مشتقة دالة التحويل بالنسبة للزمن تساوي صفر. وتكتسب هذه الخاصية كبرى في نظرية الأنظمة لإن النظام إن كان رصينا وأيضا كان خطيا فإنه يمكن تشخيص النظام كاملا وتحديد استجابته ازاء أي دخل في أي وقت وتحت مختلف الظروف بإدخال دالة النبضة (القياسية) ورصد استجابتها النبضية لإشارة الدخل. وهذا النوع من المنظومات يعرف باسم الأنظمة الخطية الرصينة.
التعريف الرياضي
لتكن , دالة دخل في منظومة رصينة و دالة خرج من ذات المنظومة. فإن زحزحة دالة الدخل بمقدار يؤدي إلى زحزحة دالة الخرج بذات المقدار. بحيث يؤدي إلى .
أمثلة
- منظومة أ: ليست رصينة لإن دالة الخرج تتغير مع الزمن وكذلك مع الدخل.
- منظومة ب: منظومة رصينة لإن الخرج يتغير حصرا مع الدخل.
طالع كذلك
مراجع
- ^ (PDF) https://web.archive.org/web/20131230235354/http://www.e-campus.ufc.dz/cours/TS_statistique/econometrie/section5-1/ch5-1-laggedex.pdf. مؤرشف من الأصل (PDF) في 2013-12-30.
{{استشهاد ويب}}: الوسيط|title=غير موجود أو فارغ (مساعدة)