دالة مطابقة
الدالة المُطابَقة أو الدالة المتطابقة أو الدالة الحيادية (بالإنجليزية: Identity function)، أو الأقتران المحايد أو المطابق، هي دالة يرتبط فيها كل عنصر بنفسه، أو يكون المجال والمجال المقابل هما نفس المجموعة.[1][2][3]
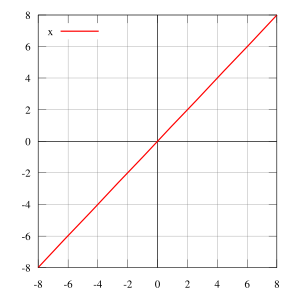
فالدالة y = f(x) = x، هي دالة محايدة.
تعريف
نقول أن دالة f محايدة، إذا حافظت على قيم المتغير. أي صارت لصور الأعداد في تلك الدالة نفس القيم.
خصائص
تعتبر خاصيات التباين والشمولية وبالتالي التقابلية من الخاصيات المميزة للدالة المحايدة، والبرهان عليها يأتي تلقائيا بعد تعويض (f(x بقيمته x.
أمثلة
إذا كان f(x)=2x+3،g(x)=½(x-3) برهن ان كلا من f5g،g5f دالة محايدة.
f5g(x)= f(g(x))
=f(½(x-3)) =2(½(x-3))+3 =x
g5f(x) =g(f(x))
=g(2x+3)
=½[(2x+3)-3]
= x
(f5g) دالة محايدة،(g5f) دالة محايدة.
- في الفضاء الشعاعي ذي البعد n، تمثل الدالة المتطابقة بالمصفوفة المتطابقة بغض النظر عن الأسس.
مراجع
- ^ Mapa، Sadhan Kumar. Higher Algebra Abstract and Linear (ط. 11th). Sarat Book House. ص. 36. ISBN:978-93-80663-24-1.
- ^ D. Marshall؛ E. Odell؛ M. Starbird (2007). Number Theory through Inquiry. Mathematical Association of America Textbooks. Mathematical Assn of Amer. ISBN:978-0883857519.
- ^ T. S. Shores (2007). Applied Linear Algebra and Matrix Analysis. Undergraduate Texts in Mathematics. Springer. ISBN:038-733-195-6. مؤرشف من الأصل في 2020-01-24.