|
تضامنًا مع حق الشعب الفلسطيني |
أرابيكا:مقالة الصفحة الرئيسية الجيدة/710
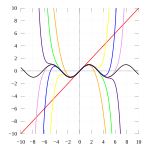
مُتَسَلْسِلَةُ تَايْلُور أو سِلْسِلَةُ تَايْلُور (بالإنجليزية: Taylor series) أو مَفْكُوكُ تَايْلُور أو نَشْرُ تَايْلُور (بالإنجليزية: Taylor expansion) لدالة ما هي مجموع غير منتهٍ من الحدود التي يُعبَّر عنها بدلالة مشتقات الدالة في نقطة محددة. تكون معظم الدوال الشائعة ومجموع متسلسلة تايلور الخاصة بها متساويتين بالقرب من هذه النقطة. سميت سلسلة تايلور على اسم العالم الإنجليزي بروك تايلور، الذي أدخلها في عام 1715. وتسمى متسلسلة تايلور أيضًا متسلسلة ماكلورين عندما تكون المشتقات عند النقطة 0، تيمنًا بالعالم الإسكتلندي كولين ماكلورين، الذي استخدم هذه الحالة الخاصة من متسلسلة تايلور على نطاق واسع في منتصف القرن الثامن عشر. المجموع الجزئي المكون من حدود n + 1 الأولى لمتسلسلة تايلور هو كثير الحدود من الدرجة n يسمى كثير حدود تايلور للدالة من الدرجة n. تعد معادلات تايلور كثيرة الحدود تقديرات تقريبية لدالة ما، والتي تصبح أكثر دقة عمومًا عندما تتزايد n. تعطي مبرهنة تايلور تقديرات كمية للخطأ الناتج عن استخدام مثل هذه التقديرات التقريبية. إذا كانت متسلسلة تايلور للدالة متقاربة، فإن مجموعها هي نهاية المتتالية اللانهائية لكثير الحدود لتايلور. قد تختلف الدالة عن مجموع متسلسلة تايلور الخاصة بها، حتى لو كانت متسلسلة تايلور متقاربة. تكون الدالة تحليلية عند نقطة x إذا كانت مساوية لمجموع متسلسلة تايلور الخاصة بها في فترة مفتوحة (أو قرص مفتوح في المستوي المركب) تحوي x. هذا يعني أن الدالة تحليلية في كل نقطة من الفترة (أو القرص).
مقالات جيدة أخرى: أمستردام – عبد الله البطال – الرياض
ما هي المقالات الجيدة؟ – بوابة رياضيات – بوابة تحليل رياضي