|
تضامنًا مع حق الشعب الفلسطيني |
ملف:Thiel-Sen estimator.svg
اذهب إلى التنقل
اذهب إلى البحث
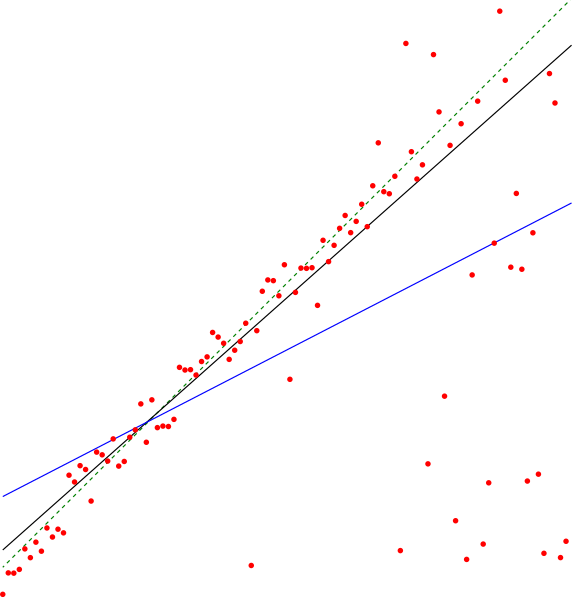
حجم معاينة PNG لذلك الملف ذي الامتداد SVG: 572 × 599 بكسل. الأبعاد الأخرى: 229 × 240 بكسل | 458 × 480 بكسل | 733 × 768 بكسل | 978 × 1٬024 بكسل | 1٬955 × 2٬048 بكسل | 2٬936 × 3٬075 بكسل.
الملف الأصلي (ملف SVG، أبعاده 2٬936 × 3٬075 بكسل، حجم الملف: 37 كيلوبايت)
تاريخ الملف
اضغط على زمن/تاريخ لرؤية الملف كما بدا في هذا الزمن.
| زمن/تاريخ | صورة مصغرة | الأبعاد | مستخدم | تعليق | |
|---|---|---|---|---|---|
| حالي | 22:59، 3 نوفمبر 2011 |  | 2٬936 × 3٬075 (37 كيلوبايت) | commonswiki>David Eppstein | Darker green, thicker lines |
استخدام الملف
ال1 ملف التالي مكررات لهذا الملف (المزيد من التفاصيل):
- ملف:Thiel-Sen estimator.svg من ويكيميديا كومنز
الصفحة التالية تستخدم هذا الملف: