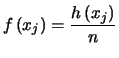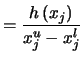إحصاء

من أرابيكا، الموسوعة الحرة
(بالتحويل من علم الاحصاء)
اذهب إلى التنقل اذهب إلى البحث
إحصاء
صنف فرعي من
جزء من
يمتهنه
عالم إحصاء (إحصائي)[1]
الموضوع
التاريخ

تعديل - تعديل مصدريحول القالب

مخطط منحنى جرسي يظهر التوزع الطبيعي الذي يستخدم في العديد من التطبيقات الإحصائية.

الإحصاء[2] (بالإنجليزية: Statistics)‏ هو أحد فروع الرياضيات الهامة ذات التطبيقات الواسعة.[3][4][5] وهو علم جمع ووصف وتفسير البيانات وبمعنى آخر صندوق الأدوات الموضوع تحت البحث التجريبي. يهتم علم الإحصاء بجمع وتلخيص وتمثيل وإيجاد استنتاجات من مجموعة البيانات المتوفرة، محاولًا التغلب على مشاكل مثل عدم تجانس البيانات وتباعدها. كل هذا يجعله ذا أهمية تطبيقية واسعة في شتى مجالات العلوم من الفيزياء إلى العلوم الاجتماعية وحتى الإنسانية، كما يلعب دورًا في السياسة والأعمال.

في تحرير البيانات، هدف العلماء لوصف فهمنا للعالم، أوصاف العلاقات المستقرة بين الظواهر الجديرة بالملاحظة على شكل نظريات أحيانًا مدعوة بأن تكون توضيحية. أي اختراع نظرية عملية مبدعة لإعادة هيكلة المعلومات التي ضمنت في إيجاد (وقبول) النظريات، وتنتزع المعلومات القابلة للاستغلال من العالم الحقيقي.

تاريخ

المقالة الرئيسية: تاريخ علم الإحصاء
جيرولامو كاردانو، من بين أقدم رواد رياضيات الاحتمالات.

تعود أقدم الكتابات حول الاحتمالات والإحصاءات إلى علماء الرياضيات وعلماء التشفير العرب، خلال العصر الذهبي الإسلامي بين القرنين الثامن والثالث عشر. كتب الخليل بن أحمد الفراهيدي (717-786) كتاب رسائل التشفير، الذي يحتوي على أول استخدام للتبديلات والتوليفات، لسرد جميع الكلمات العربية الممكنة مع وبدون حروف العلة.[6] أقدم كتاب عن الإحصاء هو أطروحة القرن التاسع عشر حول فك رموز الرسائل المشفرة، كتبها الباحث العربي الكندي (801-873). قدم الكندي في كتابه وصفًا تفصيليًا لكيفية استخدام الإحصائيات وتحليل التردد لفك تشفير الرسائل المشفرة. وضع هذا النص أسس الإحصاء وتحليل الشفرات.[7][8] قام الكندي أيضًا بأول استخدام معروف للاستدلال الإحصائي، بينما طور هو وغيره من مصممي التشفير العرب الأساليب الإحصائية المبكرة لفك تشفير الرسائل المشفرة. قدم ابن عدلان (1187-1268) فيما بعد مساهمة مهمة، في استخدام حجم العينة في تحليل التردد.[6]

يرجع تاريخ أقدم كتابات أوروبية عن الإحصاء إلى عام 1663، مع نشر Natural and Political Observations upon the Bills of Mortality لجون جرونت.[9] دارت التطبيقات المبكرة للتفكير الإحصائي حول احتياجات الدول لوضع سياستها على البيانات الديموغرافية والاقتصادية، ومن هنا جاء علم الإحصاء. اتسع نطاق تخصص الإحصاء في أوائل القرن التاسع عشر ليشمل جمع وتحليل البيانات بشكل عام. اليوم، يستخدم الإحصاء على نطاق واسع في الحكومة والأعمال والعلوم الطبيعية والاجتماعية.

وضعت الأسس الرياضية للإحصاءات الحديثة في القرن السابع عشر مع تطوير نظرية الاحتمالات بواسطة جيرولامو كاردانو وبليز باسكال وبيير دي فيرما. نشأت نظرية الاحتمال الرياضي من دراسة ألعاب الحظ، على الرغم من أن مفهوم الاحتمال قد فحص بالفعل في قانون العصور الوسطى ومن قبل فلاسفة مثل خوان كارامويل.[10] وصفت طريقة المربعات الصغرى لأول مرة بواسطة أدريان ماري ليجاندر في عام 1805.

ظهر مجال الإحصاء الحديث في أواخر القرن التاسع عشر وأوائل القرن العشرين على ثلاث مراحل.[11] كانت الموجة الأولى، في مطلع القرن، بقيادة أعمال فرانسيس جالتون وكارل بيرسون، اللذين حوَّلَ الإحصاء إلى نظام رياضي صارم يستخدم في التحليل، ليس فقط في العلوم، ولكن في الصناعة والسياسة أيضًا. تضمنت مساهمات جالتون تقديم مفاهيم الانحراف المعياري والارتباط وتحليل الانحدار وتطبيق هذه الأساليب في دراسة الخصائص المتنوعة للإنسان مثل الطول والوزن وطول رمش العين وغيرها.[12] طور بيرسون معامل الارتباط لبيرسون، والذي يُعرَّف بأنه لحظة المنتج،[13] وطريقة اللحظات لتناسب التوزيعات على العينات وتوزيع بيرسون، من بين أشياء أخرى كثيرة.[14] أسس جالتون وبيرسون Biometrika كأول مجلة للإحصاء الرياضي والإحصاء الحيوي (ثم أُطلق عليها علم القياس الحيوي)، وأسس هذا الأخير أول قسم إحصائي جامعي في العالم في كلية لندن الجامعية.[15]

صاغ رونالد فيشر مصطلح فرضية العدم أثناء تجربة تذوق الشاي للسيدة، والتي «لم يتم إثباتها أو إثباتها مطلقًا، ولكن ربما يتم دحضها أثناء التجربة».[16][17]

بدأ ويليام سيلي جوسيت الموجة الثانية من العقد الأول من القرن الماضي، وبلغت ذروتها في رؤى رونالد فيشر، الذي كتب الكتب المدرسية التي كان من المفترض أن تحدد الانضباط الأكاديمي في الجامعات حول العالم. كانت أهم منشورات فيشر هي الورقة الأساسية التي نشرها عام 1918 بعنوان العلاقة بين الأقارب على افتراض الميراث المندلي (الذي كان أول من استخدم المصطلح الإحصائي، التباين)، وعمله الكلاسيكي عام 1925، الأساليب الإحصائية لعمال البحث، وعام 1935 تصميم التجارب،[18][19][20] حيث طور تصميمًا صارمًا لنماذج التجارب. ابتكر مفاهيم الاكتفاء والإحصاء الإضافي وتحليل التمييز الخطي ومعلومات فيشر.[21] في كتابه «النظرية الوراثية للانتقاء الطبيعي» عام 1930، طبق الإحصاء على مفاهيم بيولوجية مختلفة مثل مبدأ فيشر[22] (والذي أطلق عليه أنتوني إيدوارد «ربما الحجة الأكثر شهرة في علم الأحياء التطوري») وFisherian Runaway‏[23][24][25][26][27][28] مفهوم في الانتقاء الجنسي حول تأثير ردود الفعل الإيجابية الجامح الموجود في التطور.

نشأت الموجة الأخيرة، التي شهدت بشكل أساسي صقل وتوسيع التطورات السابقة، من العمل التعاوني بين إيغون بيرسون وجيرزي نيمان في الثلاثينيات. قدموا مفاهيم خطأ «النوع الثاني» وقوة الاختبار وفترات الثقة. أظهر جيرزي نيمان في عام 1934 أن أخذ العينات العشوائية الطبقية كان بشكل عام طريقة أفضل للتقدير من أخذ العينات الهادفة (الحصص).[29]

اليوم، يتم تطبيق الأساليب الإحصائية في جميع المجالات التي تنطوي على اتخاذ القرار، لإجراء استنتاجات دقيقة من مجموعة مجمعة من البيانات ولاتخاذ القرارات في مواجهة عدم اليقين على أساس المنهجية الإحصائية. أدى استخدام أجهزة الحاسوب الحديثة إلى تسريع العمليات الحسابية الإحصائية على نطاق واسع، كما أتاح إمكانية استخدام طرق جديدة غير عملية لأداءها يدويًا. لا تزال الإحصائيات مجالًا للبحث النشط على سبيل المثال حول مشكلة كيفية تحليل البيانات الضخمة.[30]

مراحله

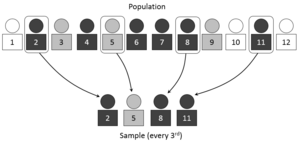
تمثيل مرئي لمعملية الاختيار العشوائيّ عن طريق تقنية اخد العينات المنهجية

الخطوة الأولى في أي عملية إحصائية هي جمع البيانات من خلال عملية الاستعيان من ضمن المجتمع الإحصائي الضخم أو من خلال تسجيل الاستجابات لمعالجة ما في تجربة (تصميم تجريبي experimental design)، أو عن طريق ملاحظة عملية متكررة مع الزمن (متسلسلات زمنية)، من ثم وضع خلاصات رقمية وتمثيلية (مخططية) graphical باستخدام ما يدعى الإحصاء الوصفي.

تُدمج الأنماط الموجودة ضمن البيانات (تنمذج) modeling لأخذ استدلالات حول مجتمعات كبيرة، لذلك يجب دراسة حجم العينة بحيث تكون ممثلة للمجتمع الإحصائي المسحوبة منه. تتم هذه العملية ضمن ما يدعى الإحصاء الاستدلالي inferential statistics ليأخذ بعين الاعتبار عشوائية وعدم دقة الملاحظات (القياسات).

غالبا ما تأخذ الاستدلالات الإحصائية شكل إجابات لأسئلة من نوع (نعم/لا) (فيما يدعى اختبار الفرضيات hypothesis testing)، تقدير خاصيات عددية (تقدير estimation)، التنبؤ prediction بملاحظات أو قياسات مستقبلية، وصف ارتباطات وعلاقات (ارتباط correlation)، أو نمذجة علاقات (انحدار regression) أو التفاف convolution.

تدخل مجمل العمليات والإجرائيات والفروع الإحصائية الموصوفة أعلاه في إطار ما يدعى الإحصاء التطبيقي، يقابله إحصاء رياضي mathematical statistics أو النظرية الإحصائية statistical theory وهي أحد فروع الرياضيات التطبيقية التي تستخدم نظرية الاحتمالات والتحليل الرياضي لوضع الممارسة الإحصائية على أساس نظري متين.

الإحصاء الوصفي

المقالة الرئيسية: إحصاء وصفي

يتضمن الإحصاء الوصفي الأدوات التي ابتكرت لتنظيم وعرض البيانات في نماذج سهلة الوصول، بمعنى آخر بطريقة ما لا تتجاوز الحدود المعرفية للعقل الإنساني، يتضمن قياسات الظواهر المتكررة، خلاصة الإحصاءات المتنوعة، المتوسطات المحسوبة بشكل رئيسي، بيانات الأسطر والإحصاءات تعرض باستعمال الجداول والرسوم البيانية. الوصف الإحصائي يعرض رؤيات مهمة لحدوث الظواهر المفردة، ويشير للمشاركة بينهم، لكن هل يمكن ليزود النتائج التي تكون القوانين المعتبرة في سياق علمي. الإحصاءات وسائل تعامل مع الاختلافات في خصائص الأشياء المتميزة، الأشياء المفردة ليست عرض بياني لمجتمع الأشياء، التي تمتلك الميزة القابلة للقياس موضع التحري، رغم تلك الاختلافات تكون نتيجة اختلاف المتغيرات الأخرى (المسيطرة والعشوائية). الفيزياء على سبيل المثال، تهتم بانتزاع والصياغة الرياضية للعلاقات المضبوطة، لا يترك مجال للتقلبات العشوائية، في إحصاءات مثل هذه التقلبات العشوائية مشكلة، العلاقات الإحصائية هكذا العلاقات التي تحدد النسبة المعينة للاختلاف الإحصائي.

الإحصاء الاستقرائي

بالمقارنة مع مناطق واسعة من الفيزياء، تلاحظ العلاقات التجريبية إحصائيا في العلوم الطبيعية، وعلم الاجتماع وعلم النفس (ومواضيع أكثر انتقائية مثل الاقتصاد). العمل التجريبي في هذه الحقول ينتقل نموذجيا على قواعد التجارب أو مسوحات العينة التجريبية، أما في حالة كامل المجتمع لا يمكن أن يلاحظ إما لأسباب عملية أو اقتصادية. الاستنتاج من العينة المحددة للأشياء لسيادة الخصائص في المجتمع هدف استنتاجي أو إحصاء استقرائي، هنا التغير يكون انعكاس التباين في العينة واجراء العينة.

الإحصاء والإجراء العلمي

اعتمادا على حالة التحقيق العلمي، البيانات مفحوصة بتغير درجات المعلومات السابقة. البيانات ستجمع لاكتشاف الظاهرة في المدخل الأول، لكنه يمكن أن يخدم الاختيار الإحصائي (التأكيد/النفي) الفرضيات حول تركيب الخاصة موضع التحري. هكذا، الإحصاء يطبق في كل مراحل العملية العلمية، حيثما الظواهر القابلة للقياس معقدة. هنا مفهومنا عام بما فيه الكفاية لاحاطة تشكيلة واسعة من المقترحات العلمية المثيرة. نأخذ على سبيل المثال اقتراح نحلة طنانة تطير، بحساب عدد الحوادث في أماكن مختلفة، نحدد حدوث الظاهرة. على هذه القاعدة، نحاول استنتاج إمكانية مصادفة نحلة، تحت الظروف المعينة (مثال يوم صيفي ممطر في برلين).

السلسلة الإحصائية

في تسجيل البيانات نولد السلسلة الإحصائية تدعى السلسلة الأصلية غير المنجزة بالبيانات الخام. نعطي مستوى مقياس ملائم (على الأقل مقياس ترتيبي)، نستطيع تصنيف البيانات الخام وهكذا نخلق سلسلة منظمة.

جمعت البيانات في نفس النقطة الزمنية أو بنفس الفترة الزمنية على عناصر مختلفة تدعى بيانات القسم المشترك.

جمعت البيانات عند نقاط مختلفة من الزمن، أو لفترات مختلفة من الزمن على نفس العنصر، تدعى بيانات السلاسل الزمنية. أن سلسلة المشاهدات مرتبة على طول الزمن.

التكرار

عدد المشاهدات التي تتطابق لفئة معطى تدعى التكرار.

الفئات مبينة لتلخيص البيانات المستمرة أو شبه المستمرة بواسطة التكرارات في البيانات المنقطعة ينظم الواحد التلاقي أو ما يسمى بالروابط، مشاهدتين أو أكثر تأخذ على نفس القيمة، لهذا لا تتطلب البيانات المنفصلة تبويب لتحسب التكرارات.

التكرار المطلق

حساب عدد المشاهدات التي تأخذ على قيمة معينة ينتج التكرار المطلق:

عندما تبوب البيانات التكرارات المطلقة للفئات محسوبة على الشكل التالي:

الخواص

التكرار النسبي

تدعى نسبة المشاهدات التي تأخذ على قيمة معينة، أو تتطابق مع فئة محددة بالتكرار النسبي. التكرار المطلق المنتج على العدد الإجمالي للمشاهدات

الخواص:

التوزيع التكراري

بتوحيد تكرارات الفئة للبيانات المبوبة بأعراض فئتهم الخاصة، جعلت التكرارات لفئات أحجام مختلفة للمقارنة، يمكن تجميع التكرارات الناتجة لتشكيل لتوزيع التكراري.

حيث حدود الفئة الدنيا والعليا.

انظر أيضًا

المراجع

  1. ^ تعريف ومعنى إحصائي في معجم المعاني الجامع نسخة محفوظة 2015-05-16 على موقع واي باك مشين.
  2. ^ Q115858366، ص. 822، QID:Q115858366
  3. ^ "Cohen (1994) The Earth Is Round (p < .05) - YourStatsGuru.com - YourStatsGuru.com". مؤرشف من الأصل في 2017-10-18.
  4. ^ Galton، F (1877). "Typical laws of heredity". Nature. ج. 15: 492–553. DOI:10.1038/015492a0.
  5. ^ Schervish، Mark J. (1995). Theory of statistics (ط. Corr. 2nd print.). New York: Springer. ISBN:0387945466.
  6. ^ أ ب Broemeling، Lyle D. (1 نوفمبر 2011). "An Account of Early Statistical Inference in Arab Cryptology". The American Statistician. ج. 65 ع. 4: 255–257. DOI:10.1198/tas.2011.10191.
  7. ^ Singh، Simon (2000). The code book : the science of secrecy from ancient Egypt to quantum cryptography (ط. 1st Anchor Books). New York: Anchor Books. ISBN:978-0-385-49532-5.
  8. ^ Ibrahim A. Al-Kadi "The origins of cryptology: The Arab contributions", Cryptologia, 16(2) (April 1992) pp. 97–126.
  9. ^ Willcox, Walter (1938) "The Founder of Statistics". Review of the المعهد الدولي للإحصاء 5(4): 321–328. قالب:Jstor
  10. ^ J. Franklin, The Science of Conjecture: Evidence and Probability before Pascal, Johns Hopkins Univ Pr 2002
  11. ^ Helen Mary Walker (1975). Studies in the history of statistical method. Arno Press. ISBN:9780405066283. مؤرشف من الأصل في 2020-07-27.
  12. ^ Galton، F (1877). "Typical laws of heredity". Nature. ج. 15 ع. 388: 492–553. Bibcode:1877Natur..15..492.. DOI:10.1038/015492a0.
  13. ^ Stigler، S.M. (1989). "Francis Galton's Account of the Invention of Correlation". Statistical Science. ج. 4 ع. 2: 73–79. DOI:10.1214/ss/1177012580.
  14. ^ Pearson، K. (1900). "On the Criterion that a given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it can be reasonably supposed to have arisen from Random Sampling". Philosophical Magazine. Series 5. ج. 50 ع. 302: 157–175. DOI:10.1080/14786440009463897. مؤرشف من الأصل في 2020-08-18.
  15. ^ "Karl Pearson (1857–1936)". Department of Statistical Science – كلية لندن الجامعية. مؤرشف من الأصل في 2008-09-25.
  16. ^ Fisher|1971|loc=Chapter II. The Principles of Experimentation, Illustrated by a Psycho-physical Experiment, Section 8. The Null Hypothesis
  17. ^ OED quote: 1935 R.A. Fisher, The Design of Experiments ii. 19, "We may speak of this hypothesis as the 'null hypothesis', and the null hypothesis is never proved or established, but is possibly disproved, in the course of experimentation."
  18. ^ Box, JF (فبراير 1980). "R.A. Fisher and the Design of Experiments, 1922–1926". ذا أمريكان ستاتيستيشين. ج. 34 ع. 1: 1–7. DOI:10.2307/2682986. JSTOR:2682986.
  19. ^ Yates, F (يونيو 1964). "Sir Ronald Fisher and the Design of Experiments". Biometrics. ج. 20 ع. 2: 307–321. DOI:10.2307/2528399. JSTOR:2528399. مؤرشف من الأصل في 2022-03-17.
  20. ^ Stanley، Julian C. (1966). "The Influence of Fisher's "The Design of Experiments" on Educational Research Thirty Years Later". American Educational Research Journal. ج. 3 ع. 3: 223–229. DOI:10.3102/00028312003003223. JSTOR:1161806. مؤرشف من الأصل في 2022-03-20.
  21. ^ Agresti، Alan؛ David B. Hichcock (2005). "Bayesian Inference for Categorical Data Analysis" (PDF). Statistical Methods & Applications. ج. 14 ع. 3: 298. DOI:10.1007/s10260-005-0121-y. مؤرشف من الأصل (PDF) في 2017-10-18.
  22. ^ Edwards، A.W.F. (1998). "Natural Selection and the Sex Ratio: Fisher's Sources". American Naturalist. ج. 151 ع. 6: 564–569. DOI:10.1086/286141. PMID:18811377.
  23. ^ Fisher, R.A. (1915) The evolution of sexual preference. Eugenics Review (7) 184:192
  24. ^ Fisher, R.A. (1930) The Genetical Theory of Natural Selection. (ردمك 0-19-850440-3)
  25. ^ Edwards, A.W.F. (2000) Perspectives: Anecdotal, Historial and Critical Commentaries on Genetics. The Genetics Society of America (154) 1419:1426
  26. ^ Andersson، Malte (1994). Sexual Selection. Princeton University Press. ISBN:0-691-00057-3. مؤرشف من الأصل في 2020-07-27.
  27. ^ Andersson, M. and Simmons, L.W. (2006) Sexual selection and mate choice. Trends, Ecology and Evolution (21) 296:302
  28. ^ Gayon, J. (2010) Sexual selection: Another Darwinian process. Comptes Rendus Biologies (333) 134:144
  29. ^ Neyman، J (1934). "On the two different aspects of the representative method: The method of stratified sampling and the method of purposive selection". Journal of the Royal Statistical Society. ج. 97 ع. 4: 557–625. DOI:10.2307/2342192. JSTOR:2342192.
  30. ^ "Science in a Complex World – Big Data: Opportunity or Threat??". Santa Fe Institute. مؤرشف من الأصل في 2016-05-30.

وصلات خارجية

مجلوبة من «https://arabica.cc/index.php?title=إحصاء&oldid=1272033»