عامل شدة الإجهاد

الإحداثيات القطبيّة عند حافة الصدع.

عامل شدة الإجهاد، $K$، يستخدم في ميكانيكا التصدع (ميكانيك الانكسار) لتوقع الحالة الإجهادية («شدة الإجهاد») قرب حافة صدع أو ثلم يتسبب به حمل خارجي أو إجهادات متبقية. هو مفهوم نظري يُطبق عادةً على مواد متجانسة مرنة خطيًّا وهو مفيد لتوفير معيار يقيس حد الانهيار (الفشل الميكانيكي) للمواد الهشة، وهو أسلوب أساسي في فرع تسامحات الأضرار. يمكن تطبيق المفهوم أيضًا على المواد التي تشهد ظاهرة خضوع (انسياب) بمقياس صغير عند حافة الصدع.

تعتمد شدة $K$ على هندسة العينة، وحجم الصدع أو الثلم وموقعهما، وشدة الأحمال وتنوع أوضاعها على المادة.

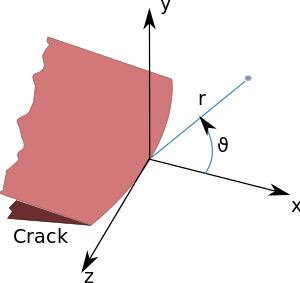
تتنبأ نظرية المرونة الخطية أن توزع الإجهادات (${\sigma }_{ij}$) قرب حافة الصدع، بالإحداثيات القطبية ($r,\theta$$r,\theta$$r,\theta$) عند وضع مبدأ الإحداثيات عند حافة الصدع، يأخذ الشكل التالي:

${\sigma }_{ij}(r,\theta )=\frac{K}{\sqrt{2\pi r}}{f}_{ij}(\theta )+\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{s}$

حيث $K$ معامل شدة الإجهاد (بواحدة الإجهاد × الطول^0.5) و$f_{ij}$ الكمية اللابعدية التي تتغير مع الحمل والشكل الهندسي. نظريًّا، عند تناهي $r$ إلى الصفر، يسعى الإجهاد ${\sigma }_{ij}$ نحو $\mathrm{\infty }$ ما يسبب نقطة شاذة (متفردة رياضية) للإجهاد. لكن عمليًّا، تنهار هذه العلاقة قرب الحافة ($r$ صغيرة) بسبب حدوث لدونة عادةً عند إجهادات تتجاوز حد خضوع (انسياب) المادة ولا يمكن تطبيق الحل المرن الخطي عندها. مع ذلك، إذا كانت المنطقة اللدنة عند حافة الصدع صغيرةً مقارنةً بطول الصدع، يظل من الممكن تطبيق توزع الإجهادات المقارب قرب حافة الصدع عندها.

عوامل شدة الإجهاد لعدة أوضاع

تستخدم ثلاثة أوضاع مستقلة خطيًّا في ميكانيك الانكسار (ميكانيكا التصدع). تسمى أنواع التحميل هذه الوضع الأول والثاني والثالث على التتالي. الوضع الأول هو وضع فتح (شد) يتباعد فيه سطحا الصدع مباشرةً عن بعضهما البعض. الوضع الثاني هو وضع انزلاق (قص في المستوي) ينزلق فيه سطحا الصدع فوق بعضهما البعض باتجاه عمودي على الحافة القائدة للصدع. الوضع الثالث وضع تشقق (قص فراغي أو قص متعدد المستويات) يتحرك فيه سطحا الصدع بالنسبة لبعضهما البعض بشكل موازٍ للحافة القائدة للصدع. الوضع الأول هو الأكثر شيوعًا في التصاميم الهندسية.

تستخدم أرقام دلالية مختلفة لتخصيص عامل شدة الإجهاد للأوضاع الثلاثة المختلفة، عامل شدة الإجهاد للوضع الأول يرمز له $K_{\mathrm{I}}$ ويطبق على وضع انفتاح الصدع. عامل شدة الإجهاد للوضع الثاني $K_{\mathrm{I}\mathrm{I}}$، يطبق على وضع انزلاق الصدع، أما عامل شدة الإجهاد للوضع الثالث $K_{\mathrm{I}\mathrm{I}\mathrm{I}}$، يطبق على وضع التمزق. تعرّف هذه العوامل بشكل رسمي على أنها على التتالي:

$\begin{array}{ll}{K}_{\mathrm{I}}& =\underset{r\to 0}{\lim }\sqrt{2\pi r}{\sigma }_{yy}(r,0)\\ K_{\mathrm{I}\mathrm{I}}& =\underset{r\to 0}{\lim }\sqrt{2\pi r}{\sigma }_{yx}(r,0)\\ K_{\mathrm{I}\mathrm{I}\mathrm{I}}& =\underset{r\to 0}{\lim }\sqrt{2\pi r}{\sigma }_{yz}(r,0).\end{array}$

علاقة العامل بمعدل تحرير الطاقة وتكامل المسار الحدودي

في شروط الإجهاد المستوي، يكون معدل تحرير طاقة الانفعال ($G$) لأجل صدع يخضع للتحميل من الوضع الأول الصافي أو الوضع الثاني الصافي متعلقًا بعامل شدة الإجهاد وفق:

$G_{\mathrm{I}}=K_{\mathrm{I}}^2\left(\frac{1}{E}\right)$

$G_{\mathrm{I}\mathrm{I}}=K_{\mathrm{I}\mathrm{I}}^2\left(\frac{1}{E}\right)$

حيث$E$ معامل يونغ و $\nu$ نسبة بواسون (معامل بواسون) للمادة. يفترض أن المادة متناظرة (إيزوتروبية)، ومتجانسة، ومرنة خطيًّا. افتُرض أن الصدع يمتد على اتجاه الصدع الابتدائي.

لأجل شروط الانفعال المستوي، تكون العلاقة المكافئة أكثر تعقيدًا بقليل:

$G_{\mathrm{I}}=K_{\mathrm{I}}^2\left(\frac{1-{\nu }^2}{E}\right)$

$G_{\mathrm{I}\mathrm{I}}=K_{\mathrm{I}\mathrm{I}}^2\left(\frac{1-{\nu }^2}{E}\right).$

للتحميل وفق الوضع الثالث الصافي:

$G_{\mathrm{I}\mathrm{I}\mathrm{I}}=K_{\mathrm{I}\mathrm{I}\mathrm{I}}^2\left(\frac{1}{2\mu }\right)=K_{\mathrm{I}\mathrm{I}\mathrm{I}}^2\left(\frac{1+\nu }{E}\right)$

حيث $\mu$ معامل القص. يبقى الجمع الخطي صحيحًا عند التحميل العام في الانفعال المستوي :

$G=G_{\mathrm{I}}+G_{\mathrm{I}\mathrm{I}}+G_{\mathrm{I}\mathrm{I}\mathrm{I}}.$

يمكن الحصول على علاقة مشابهة للانفعال المستوي بإضافة إسهامات الأوضاع الثلاث.

يمكن استخدام العلاقات السابقة أيضًا للربط بين تكامل المسار الحدودي (التكامل جيه) وعامل شدة الإجهاد لأن:

$G=J={\int }_{\mathrm{\Gamma }}(Wd{x}_2-\mathbf{t}\cdot \frac{\partial \mathbf{u}}{\partial x_1}ds).$

عامل شدة الإجهاد الحرج

عامل شدة الإجهاد، $K$، بارامتر يضخم شدة الجهد المطبق الذي يتضمن البارامتر الهندسي $Y$ (نوع الحمل). تتناسب شدة الإجهاد في أي وضع تناسبًا طرديًّا مباشرًا مع الحمل المطبق على المادة. إن أمكن صنع صدع حاد جدًّا أو ثلم على شكل حرف فّي في مادة، يمكن تحديد القيمة الأصغرية للمقدار $K_{\mathrm{I}}$ تجريبيًّا، وهي القيمة الحرجة (الحدية) لعامل شدة الإجهاد المطلوبة لتشكيل الصدع. تسمى هذه القيمة الحرجة المحددة للتحميل بالوضع الأول في الانفعال المستوي باسم حد المتانة الحرج ($K_{\mathrm{I}\mathrm{c}}$) للمادة. $K_{\mathrm{I}\mathrm{c}}$ له واحدة الإجهاد مضروبًا بجذر المسافة (أي MN/m^3/2). تشير واحدات $K_{\mathrm{I}\mathrm{c}}$ إلى أن إجهاد الكسر للمادة يجب أن يحدث قبل مسافة ما حرجة لكي تصل القيمة إلى $K_{\mathrm{I}\mathrm{c}}$ ويحدث تشكل الصدع. عامل شدة الإجهاد الحرج للوضع الأول،$K_{\mathrm{I}\mathrm{c}}$، هو أكثر بارامتر تصميمي استعمالًا في ميكانيك الانكسار ولذلك يجب فهمه إذا أردنا تصميم مواد لها سماحية للتصدعات كما في الجسور، والأبنية، والطيارات، وحتى الأجراس.

لا يمكن للتجليخ (التلميع) اكتشاف الصدوع. عادةً، إذا كان بالإمكان رؤية الصدع فهو في حالة قريبة جدًّا من حالة الإجهاد الحرج التي يتنبأ بها عامل شدة الإجهاد.

المعيار جي

المعيار جي (بالإنجليزية: G-criterion)‏ معيار تصدع يصف علاقة عامل شدة الإجهاد الحرج (أو حد المتانة) بعوامل شدة الإجهاد للأوضاع الثلاثة. يكتب معيار الانهيار هذا كالتالي:

$K_{\mathrm{c}}^2=K_{\mathrm{I}}^2+K_{\mathrm{I}\mathrm{I}}^2+\frac{E^{\prime }}{2\mu }{K}_{\mathrm{I}\mathrm{I}\mathrm{I}}^2$

حيث $K_{\mathrm{c}}$ حد المتانة، $E^{\prime }=E/(1-{\nu }^2)$ للانفعال المستوي و$E^{\prime }=E$ للإجهاد المستوي. يُكتب عامل شدة الإجهاد الحدي للإجهاد المستوي عادةً $K_{\mathrm{c}}$.

أمثلة

صفيحة لا نهائية: إجهاد وحيد البعد متوزع بانتظام

عامل شدة الإجهاد لصدع مستقيم مفترض طوله $2a$ عمودي على اتجاه التحميل، في مستوٍ لانهائي، له حقل إجهاد منتظم $\sigma$ يعطى بالعلاقة:

$K_{\mathrm{I}}=\sigma \sqrt{\pi a}$

تشقق على شكل قطعة نقدية في مجال لا نهائي

عامل شدة الإجهاد عند حافة تشقق على شكل قطعة نقدية نصف قطرها $a$ في مجال لانهائي خاضع لإجهاد شد وحيد البعد $\sigma$ هو:

$K_{\mathrm{I}}=\frac{2}{\pi }\sigma \sqrt{a\pi }.$

صفيحة محدودة: إجهاد وحيد البعد متوزع بانتظام

إذا توضع الصدع مركزيًّا على صفيحة محدودة عرضها $2b$ وارتفاعها $2h$، يعطى عامل شدة الإجهاد بالعلاقة التقريبية التالية:

$K_{\mathrm{I}}=\sigma \sqrt{\pi a}\left[\frac{1-\frac{a}{2b}+0.326{\left(\frac{a}{b}\right)}^2}{\sqrt{1-\frac{a}{b}}}\right].$

إذا لم يكن الصدع مركزيًّا بالنسبة للعرض، أي أن $d\ne b$، يمكن تقريب قيمة عامل شدة الإجهاد عند الموضع A من خلال منشور السلسلة:

$K_{\mathrm{I}\mathrm{A}}=\sigma \sqrt{\pi a}[1+\sum _{n=2}^M{C}_n{\left(\frac{a}{b}\right)}^n]$

حيث يمكن إيجاد العوامل $C_n$ من خلال الملاءمة مع منحنيات شدة الإجهاد لأجل العديد من قيم $d$. يمكن إيجاد علاقة مشابهة (ولكن غير متطابقة) لأجل الحافة B من الصدع. من العلاقات البديلة لعوامل شدة الإجهاد عند A وB:

$K_{\mathrm{I}\mathrm{A}}=\sigma \sqrt{\pi a}{\mathrm{\Phi }}_A,K_{\mathrm{I}\mathrm{B}}=\sigma \sqrt{\pi a}{\mathrm{\Phi }}_B$

حيث

$\begin{array}{ll}{\mathrm{\Phi }}_A& :=[\beta +\left(\frac{1-\beta }{4}\right){(1+\frac{1}{4\sqrt{\sec {\alpha }_A}})}^2]\sqrt{\sec {\alpha }_A}\\ {\mathrm{\Phi }}_B& :=1+\left[\frac{\sqrt{\sec {\alpha }_{AB}}-1}{1+0.21\sin \left\{8{\tan }^{}\left[{\left(\frac{{\alpha }_A-{\alpha }_B}{{\alpha }_A+{\alpha }_B}\right)}^{0.9}\right]\right\}}\right]\end{array}$

مع

$\beta :=\sin \left(\frac{\pi {\alpha }_B}{{\alpha }_A+{\alpha }_B}\right),{\alpha }_A:=\frac{\pi a}{2d},{\alpha }_B:=\frac{\pi a}{4b-2d};{\alpha }_{AB}:=\frac{4}{7}{\alpha }_A+\frac{3}{7}{\alpha }_B.$

في العلاقات السابقة: $d$ هي المسافة من مركز التشقق (الصدع) إلى النقطة المحيطية الأقرب A. لاحظ أنه عندما $d=b$ لا يمكن تبسيط العلاقات السابقة إلى العلاقة التقريبية لصدع متمركز.

تشقق طرفي في صفيحة خاضعة لإجهاد وحيد البعد

لأجل صفيحة لها الأبعاد $2h\times b$ تحوي فيها تشققًا طرفيًا غير مقيد طوله $a$، إذا كانت أبعاد الصفيحة تحقق $h/b\ge 0.5$ و$a/b\le 0.6$، يكون عامل شدة الإجهاد عند طرف التشقق الخاضع لإجهاد وحيد البعد $\sigma$:

$K_{\mathrm{I}}=\sigma \sqrt{\pi a}[1.122-0.231\left(\frac{a}{b}\right)+10.55{\left(\frac{a}{b}\right)}^2-21.71{\left(\frac{a}{b}\right)}^3+30.382{\left(\frac{a}{b}\right)}^4].$

لأجل الوضع الذي يحقق $h/b\ge 1$ و$a/b\ge 0.3$، يمكن تقريب عامل شدة الإجهاد إلى:

$K_{\mathrm{I}}=\sigma \sqrt{\pi a}\left[\frac{1+3\frac{a}{b}}{2\sqrt{\pi \frac{a}{b}}{(1-\frac{a}{b})}^{3/2}}\right].$

تستخدم العينات الخاضعة لهذه الشروط بشكل شائع في اختبارات حد المتانة.

صفيحة لا نهائية: صدع مائل في حقل إجهادات ثنائي البعد

لأجل صدع مائل طوله $2a$ في حقل إجهادات ثنائي البعد بإجهاد $\sigma$ في اتجاه المحور $y$ (اتجاه العينات) وإجهاد $\alpha \sigma$ في اتجاه المحور $x$ (اتجاه السينات)، عوامل شدة الإجهاد هي:

$\begin{array}{ll}{K}_{\mathrm{I}}& =\sigma \sqrt{\pi a}({\cos }^2\beta +\alpha {\sin }^2\beta )\\ K_{\mathrm{I}\mathrm{I}}& =\sigma \sqrt{\pi a}(1-\alpha )\sin \beta \cos \beta \end{array}$

حيث $\beta$ الزاوية التي يصنعها الصدع مع محور $x$.

صدع في صفيحة خاضع لقوة نقطية في داخل المستوي

لنأخذ صفيحة أبعادها $2h\times 2b$ تحتوي صدعًا طوله $2a$. تطبق قوة نقطية مركباتها $F_x$ و$F_y$ على النقطة ($x,y$) من الصفيحة.

للحالة التي تكون فيها الصفيحة كبيرة مقارنةً بحجم الصدع ونقطة تأثير القوة قريبة نسبيًّا من الصدع -أي $h\gg a$, $b\gg a$, $x\ll b$, $y\ll h$$y\ll h$ - يمكن اعتبار الصفيحة لا نهائية. في هذه الحالة عوامل شدة الإجهاد للمركبة $F_x$ عند طرف الصدع B ($x=a$$x=a$$x=a$$x=a$) هي:

$\begin{array}{ll}{K}_{\mathrm{I}}& =\frac{F_x}{2\sqrt{\pi a}}\left(\frac{\kappa -1}{\kappa +1}\right)[G_1+\frac{1}{\kappa -1}{H}_1]\\ K_{\mathrm{I}\mathrm{I}}& =\frac{F_x}{2\sqrt{\pi a}}[G_2+\frac{1}{\kappa +1}{H}_2]\end{array}$

حيث

$\begin{array}{ll}{G}_1& =1-\text{Re}\left[\frac{a+z}{\sqrt{z^2-a^2}}\right],G_2=-\text{Im}\left[\frac{a+z}{\sqrt{z^2-a^2}}\right]\\ H_1& =\text{Re}\left[\frac{a(\overline{z}-z)}{(\overline{z}-a)\sqrt{{\overline{z}}^2-a^2}}\right],H_2=-\text{Im}\left[\frac{a(\overline{z}-z)}{(\overline{z}-a)\sqrt{{\overline{z}}^2-a^2}}\right]\end{array}$

مع $z=x+iy$, $\overline{z}=x-iy$, $\kappa =3-4\nu$ للانفعال المستوي، و$\kappa =(3-\nu )/(1+\nu )$ للإجهاد المستوي، و$\nu$ معامل بواسون (نسبة بواسون). يكون عامل شدة الإجهاد للمركبة $F_y$ عند الطرف B محددًا وفق:

$\begin{array}{ll}{K}_{\mathrm{I}}& =\frac{F_y}{2\sqrt{\pi a}}[G_2-\frac{1}{\kappa +1}{H}_2]\\ K_{\mathrm{I}\mathrm{I}}& =-\frac{F_y}{2\sqrt{\pi a}}\left(\frac{\kappa -1}{\kappa +1}\right)[G_1-\frac{1}{\kappa -1}{H}_1].\end{array}$

يمكن تحديد عوامل شدة الإجهاد عند الطرف A ($x=-a$) من العلاقات السابقة. لأجل الحمل $F_x$ المؤثر على النقطة $(x,y)$:

$K_{\mathrm{I}}(-a;x,y)=-K_{\mathrm{I}}(a;-x,y),K_{\mathrm{I}\mathrm{I}}(-a;x,y)=K_{\mathrm{I}\mathrm{I}}(a;-x,y).$

وبشكل مشابه لأجل الحمل $F_y$$K_{\mathrm{I}}(-a;x,y)=K_{\mathrm{I}}(a;-x,y),K_{\mathrm{I}\mathrm{I}}(-a;x,y)=-K_{\mathrm{I}\mathrm{I}}(a;-x,y).$

انظر أيضًا

• ميكانيكا تصدع
• حد المتانة
• معدل انبعاث طاقة الإجهاد
• نظرية فشل المواد
• تركيز الإجهاد